Square-free word

In combinatorics, a square-free word is a word (a sequence of characters) that does not contain any subword twice in a row.

Thus a square-free word is one that avoids the pattern XX.

Examples

Over a two-letter alphabet {a, b} the only square-free words are the empty word and a, b, ab, ba, aba, and bab. However, there exist infinite square-free words in any alphabet with three or more symbols, as proved by Axel Thue.

One example of an infinite square-free word over an alphabet of size 3 is the word over the alphabet {0,±1} obtained by taking the first difference of the Thue–Morse sequence. That is, from the Thue–Morse sequence

0, 1, 1, 0, 1, 0, 0, 1, 1, 0, 0, 1, 0, 1, 1, 0, ...

one forms a new sequence in which each term is the difference of two consecutive terms of the Thue–Morse sequence. The resulting square-free word is

1, 0, −1, 1, −1, 0, 1, 0, −1, 0, 1, −1, 1, 0, −1, ... (sequence A029883 in OEIS).

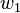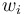Another example found by John Leech is defined recursively over the alphabet {a, b, c}. Let $w_1$ be any word starting with the letter a. Define the words $\{w_i \mid i \in \mathbb{N} \}$ recursively as follows: the word $w_{i+1}$ is obtained from $w_i$ by replacing each a in 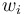$w_i$ with abcbacbcabcba, each b with bcacbacabcacb, and each c with cabacbabcabac. It is possible to check that the sequence converges to the infinite square-free word

abcbacbcabcbabcacbacabcacbcabacbabcabacbcacbacabcacb...

Related concepts

A cube-free word is one with no occurrence of www for a factor w. The Thue-Morse sequence is an example of a cube-free word over a binary alphabet. This sequence is not square-free but is "almost" so: the critical exponent is 2. The Thue–Morse sequence has no overlap or overlapping square, instances of 0X0X0 or 1X1X1: it is essentially the only infinite binary word with this property.

The Thue number of a graph G is the smallest number k such that G has a k-coloring for which the sequence of colors along every non-repeating path is squarefree.

The Kolakoski sequence is an example of a cube-free sequence.

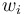An abelian p-th power is a subsequence of the form $w_1 \cdots w_p$ where each $w_i$ is a permutation of 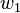$w_1$. There is no abelian-square-free infinite word over an alphabet of size three: indeed, every word of length eight over such an alphabet contains an abelian square. There is an infinite abelian-square-free word over an alphabet of size five.

References

• .