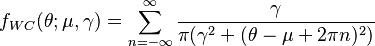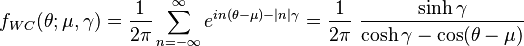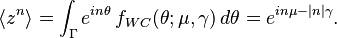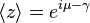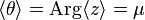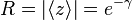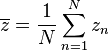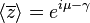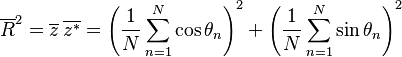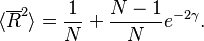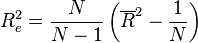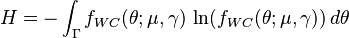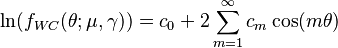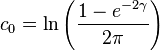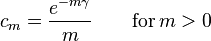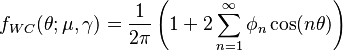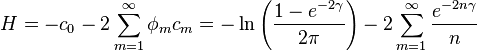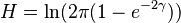Wrapped Cauchy distribution
|
Probability density function
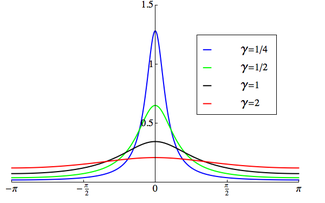 The support is chosen to be [-π,π) |
|
|
Cumulative distribution function
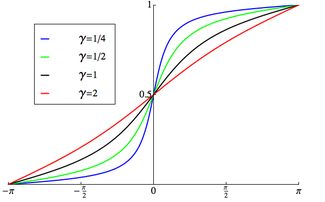 The support is chosen to be [-π,π) |
|
| Parameters | 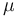 Real Real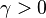 |
|---|---|
| Support | 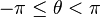 |
 |
|
| CDF |  |
| Mean | 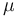 (circular) (circular) |
| Variance | 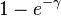 (circular) (circular) |
| Entropy | 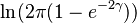 (differential) (differential) |
| CF | 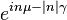 |
In probability theory and directional statistics, a wrapped Cauchy distribution is a wrapped probability distribution that results from the "wrapping" of the Cauchy distribution around the unit circle. The Cauchy distribution is sometimes known as a Lorentzian distribution, and the wrapped Cauchy distribution may sometimes be referred to as a wrapped Lorentzian distribution.
The wrapped Cauchy distribution is often found in the field of spectroscopy where it is used to analyze diffraction patterns (e.g. see Fabry–Pérot interferometer)
Description
The probability density function of the wrapped Cauchy distribution is:[1]
where  is the scale factor and
is the scale factor and 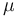 is the peak position of the "unwrapped" distribution. Expressing the above pdf in terms of the characteristic function of the Cauchy distribution yields:
is the peak position of the "unwrapped" distribution. Expressing the above pdf in terms of the characteristic function of the Cauchy distribution yields:
In terms of the circular variable 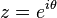 the circular moments of the wrapped Cauchy distribution are the characteristic function of the Cauchy distribution evaluated at integer arguments:
the circular moments of the wrapped Cauchy distribution are the characteristic function of the Cauchy distribution evaluated at integer arguments:
where 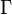 is some interval of length
is some interval of length 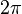 . The first moment is then the average value of z, also known as the mean resultant, or mean resultant vector:
. The first moment is then the average value of z, also known as the mean resultant, or mean resultant vector:
The mean angle is
and the length of the mean resultant is
Estimation of parameters
A series of N measurements 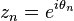 drawn from a wrapped Cauchy distribution may be used to estimate certain parameters of the distribution. The average of the series
drawn from a wrapped Cauchy distribution may be used to estimate certain parameters of the distribution. The average of the series 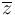 is defined as
is defined as
and its expectation value will be just the first moment:
In other words, 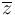 is an unbiased estimator of the first moment. If we assume that the peak position
is an unbiased estimator of the first moment. If we assume that the peak position 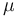 lies in the interval
lies in the interval  , then Arg
, then Arg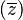 will be a (biased) estimator of the peak position
will be a (biased) estimator of the peak position 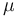 .
.
Viewing the 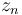 as a set of vectors in the complex plane, the
as a set of vectors in the complex plane, the 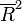 statistic is the length of the averaged vector:
statistic is the length of the averaged vector:
and its expectation value is
In other words, the statistic
will be an unbiased estimator of 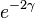 , and
, and 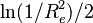 will be a (biased) estimator of
will be a (biased) estimator of  .
.
Entropy
The information entropy of the wrapped Cauchy distribution is defined as:[1]
where 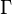 is any interval of length
is any interval of length 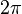 . The logarithm of the density of the wrapped Cauchy distribution may be written as a Fourier series in
. The logarithm of the density of the wrapped Cauchy distribution may be written as a Fourier series in 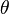 :
:
where
which yields:
(c.f. Gradshteyn and Ryzhik [2] 4.224.15) and
(c.f. Gradshteyn and Ryzhik [2] 4.397.6). The characteristic function representation for the wrapped Cauchy distribution in the left side of the integral is:
where 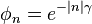 . Substituting these expressions into the entropy integral, exchanging the order of integration and summation, and using the orthogonality of the cosines, the entropy may be written:
. Substituting these expressions into the entropy integral, exchanging the order of integration and summation, and using the orthogonality of the cosines, the entropy may be written:
The series is just the Taylor expansion for the logarithm of 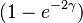 so the entropy may be written in closed form as:
so the entropy may be written in closed form as:
See also
- Wrapped distribution
- Dirac comb
- Wrapped normal distribution
- Circular uniform distribution
- McCullagh's parametrization of the Cauchy distributions
References
- ↑ 1.0 1.1 Lua error in package.lua at line 80: module 'strict' not found.
- ↑ 2.0 2.1 Lua error in package.lua at line 80: module 'strict' not found.
- Lua error in package.lua at line 80: module 'strict' not found.
- Lua error in package.lua at line 80: module 'strict' not found.