X-ray standing waves
The X-ray standing wave (XSW) technique can be used to study the structure of surfaces and interfaces with high spatial resolution and chemical selectivity. Pioneered by B.W. Batterman in the 1960s [1] the availability of synchrotron light has stimulated the application of this interferometric technique to a wide range of problems in surface science.[2][3]
Basic principles
An X-ray interference field created by Bragg reflection provides the length scale against which atomic distances can be measured. The spatial modulation of this field described by the dynamical theory of X-ray diffraction undergoes a pronounced change when the sample is scanned through the Bragg condition. Due to a relative phase variation between the incoming and the reflected beam the nodal planes of the XSW field shift by half a lattice constant.[4]
Depending on the position of the atoms within this wave field the element specific absorption of X-rays varies in a characteristic way. Therefore, measurement of the photo yield – via X-ray fluorescence or photoelectron spectroscopy – can reveal the position of the atoms relative to the lattice planes.
For a quantitative analysis the normalized photo yield  is described by [2][3]
is described by [2][3]
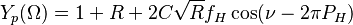 ,
,
where 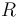 is the reflectivity and
is the reflectivity and  is the relative phase of the interfering beams. The characteristic shape of
is the relative phase of the interfering beams. The characteristic shape of  can be used to derive precise structural information about the surface atoms because the two parameters
can be used to derive precise structural information about the surface atoms because the two parameters 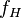 (coherent fraction) and
(coherent fraction) and  (coherent position) are directly related to the Fourier representation of the atomic distribution function.
(coherent position) are directly related to the Fourier representation of the atomic distribution function.
Selected applications
which require ultra-high vacuum conditions
- Physisorption and chemisorption studies [2][3]
- Diffusion of dopants in crystals [6]
- Superlattices and Quasi-crystal characterization
which do not require ultra-high vacuum conditions
- Langmuir-Blodgett films
- Self-assembled monolayers
- Buried interfaces
See also
References
- ↑ B. W. Batterman and H. Cole, Dynamical Diffraction of X Rays by Perfect Crystals, Rev. Mod. Phys. 36 (1964) 681
- ↑ 2.0 2.1 2.2 J. Zegenhagen, Surface structure determination with X-ray standing waves Surf. Sci. Rep. 18(7/8) (1993) 199
- ↑ 3.0 3.1 3.2 D. P. Woodruff, Surface structure determination using x-ray standing waves, Rep. Prog. Phys. 68(4) (2005) 743
- ↑ J. Als-Nielsen and D. McMorrow, Elements of Modern X-ray Physics, John Wiley & Sons, Ltd. (2000)
- ↑ L. Cheng, P. Fenter, M. J. Bedzyk, and N. J. Sturchio, Fourier-Expansion Solution of Atom Distributions in a Crystal Using X-Ray Standing Waves, Phys. Rev. Lett. 90 (2003) 255503
- ↑ P. Hoenicke et al., Depth profile characterization of ultra shallow junction implants, Anal. Bioanal. Chem., 396 (8), 2825-2832 (2010)
Further reading
Lua error in package.lua at line 80: module 'strict' not found.