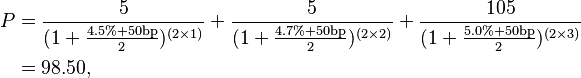Z-spread

The Z-spread, ZSPRD, Zero-volatility spread or Yield curve spread of a mortgage-backed security (MBS) is the parallel shift or spread over the zero-coupon Treasury yield curve required for discounting a pre-determined cash flow schedule to arrive at its present market price. The Z-spread is also widely used in the credit default swap (CDS) market as a measure of credit spread that is relatively insensitive to the particulars of specific corporate or government bonds.

Since the Z-spread uses the entire yield curve to value the individual cash flows of a bond, it provides a more-realistic valuation than an interpolated yield spread based on a single point of the curve, such as the bond's final maturity date or weighted-average life. However, the Z-spread does not incorporate variability in cash flows, so a fuller valuation of a rate-dependent security often requires the more-realistic (and more-complicated) option-adjusted spread.

Definition

For mortgage-backed securities, a projected prepayment rate tends to be stated; for example, the PSA assumption for a particular MBS might equate a particular group of mortgages to an 8-year amortizing bond with 6% mortality per annum. This gives a single series of nominal cash flows, as if the MBS were a riskless bond. If these payments are discounted to net present value (NPV) with a riskless zero-coupon Treasury yield curve, the sum of their values will tend to overestimate the market price of the MBS. This difference arises because the MBS market price incorporates additional factors such as liquidity and credit risk and embedded option cost. The Z-spread of a bond is the number of basis points (bp) that one needs to add to the Treasury yield curve (or technically to Treasury forward rates), so that the NPV of the bond cash flows (using the adjusted yield curve) equals the market price of the bond (including accrued interest). The spread is calculated iteratively.

Example

Assume that on 7/1/2008:

• A bond has three future cash flows: $5 on 7/1/2009; $5 on 7/1/2010; $105 on 7/1/2011.
• The corresponding zero-coupon Treasury rates (compounded semi-annually) are: 4.5% for 7/1/2009; 4.7% for 7/1/2010; 5.0% for 7/1/2011.
• The bond's accrued interest is 0.
• The Z-spread is 50 bp.

Then the price P of this bond on 7/1/2008 is given by:

$\begin{align} P & = \frac{5}{(1 + \frac{4.5\% + 50\mathrm{bp}}{2})^{(2 \times 1)}} + \frac{5}{(1 + \frac{4.7\% + 50\mathrm{bp}}{2})^{(2 \times 2)}} + \frac{105}{(1 + \frac{5.0\% + 50\mathrm{bp}}{2})^{(2 \times 3)}} \\ & = 98.50, \\ \end{align}$

where (for simplicity) the calculation has ignored the slight difference between parallel shifts of spot rates and forward rates.

Benchmark for CDS basis

The Z-spread is widely used as the "cash" benchmark for calculating the CDS basis. The CDS basis is commonly the CDS fee minus the Z-spread for a fixed-rate cash bond of the same issuer and maturity. For instance, if a corporation's 10-year CDS is trading at 200 bp and the Z-spread for the corporation's 10-year cash bond is 287 bp, then its 10-year CDS basis is –87 bp.

See also

• Option-adjusted spread
• I-spread

References

• Frank J. Fabozzi, The Handbook of Fixed Income Securities, 7th edition; McGraw-Hill, 2005