Algebra

Kvadratinės lygties $ax^{2}+bx+c=0$ sprendinys, koeficientai $a,b,c$, čia $a$ yra nelygus $0$.

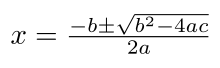
Algebra (arab. ‏الجبر‎ = al-jabr – atstatymas, atitaisymas) – matematikos šaka, tirianti veiksmų su įvairiais dydžiais (reiškiamais raidėmis) bendrąsias savybes, nepriklausomas nuo tų dydžių kilmės.

Algebroje sprendžiami dydžių sistemose kylantys uždaviniai, kai dydžių sistemos klasifikuojamos pagal veiksmų savybes. Skirtingai nei matematinėje analizėje ar funkcijų teorijoje, algebroje nėra ribos sąvokos.

Pagal algebrines sistemas – elementų aibes, kurioms apibrėžti veiksmai ir jų atlikimo taisyklės (pvz., grupė, žiedas, kūnas) – algebra skirstoma į smulkesnes šakas:

• Tiesinė algebra, tirianti tiesines erdves
• Grupių teorija, tirianti grupes bei jų savybes
• Kūnų teorija, tirianti kūnų plėtinius:
  • Algebrinių lygčių teorija
  • Algebrinių skaičių kūnų teorija
  • Algebrinių funkcijų kūnų teorija
• Žiedų teorija, tirianti žiedų struktūrą ir savybes
  • Idealų teorija
  • Algebrų teorija
  • Normuotoji algebra
• Struktūrų teorija, tirianti algebrines sistemas, kuriose sudėtis ir daugyba yra komutatyvios bei asociatyvios operacijos (struktūras).

Istorija

Algebra yra viena seniausių matematikos šakų, atsiradusi senovės Rytų civilizacijose, kur buvo ieškoma apibendrintų metodų panašiems uždaviniams spręsti. Algebros ištakų randama 4000 metų senumo rankraščiuose iš Babilonijos, Egipto, Indijos, Kinijos. Antikinėje Graikijoje algebrinius uždavinius reikšdavo geometriškai, tik apie 250 m. Diogantas pamėgino atskirti algebrą nuo geometrijos.

Jau VI amžiuje indų matematikai naudojo nulį ir neigiamus skaičius, nežinomųjų dydžių žymėjimą, o 825 m. Chorizmi išleista „Knyga apie atstatymą ir priešpastatymą“ laikytina pirmuoju algebros vadovėliu. Iš atstatymą reiškiančio arabiško žodžio al – jabr („al džabr“) kilo ir algebros pavadinimas.

Iki XVI a. algebra daugiausiai naudota tik lygčių sprendimui. XVI a. prie sparčios algebros pažangos prisidėjo italų matematikai N. Tartaglia, G. Cordano, L. Ferrari, o prancūzas Fransua Vijetas (1540–1603) sutvarkė algebros simboliką. 1637 m. Renė Dekartas išleido veikalą La Géométrie, kuriame pristatė savo analizinės geometrijos atradimą ir priėmė dabartinį algebros žymėjimą.

1799 m. vokiečių matematikas F. Gausas įrodė pagrindinę algebros teoremą. XIX a. pirmoje pusėje N. Abelis ir E. Galois ženkliai prisidėjo prie algebros vystymo, taip pat pradėjo naudoti visai naujas sąvokas, kurios dabar sudaro grupių, kūnų, žiedų ir struktūrų teorijų pagrindą.

Pirmasis į Lietuvą pakliuvęs algebros vadovėlis – 1733 m. Alpha matheseos, pagal kurį Vilniaus universitete algebra dėstyta nuo XVIII a. antrosios pusės. Pirmas vadovėlis lietuvių kalba – M. Šikšnio Elementarinė algebra, išleistas 1921–1926 m.