Okrąg jednostkowy
Okrąg jednostkowy – wieloznaczne pojęcie matematyczne:
- okrąg o promieniu jednostkowym, tzn. równym 1[1][2];
- okrąg w kartezjańskim układzie współrzędnych o środku jego w początku, tzn. punkcie i promieniu 1[3];
- zbiór liczb zespolonych o jednostkowym module: [4][5]. Nazwa jest związana z obrazem tego zbioru na płaszczyźnie zespolonej.
Ostatni z tych zbiorów jest grupą ze względu na mnożenie, nazywaną grupą okręgu[4].
Często oznacza się go symbolem a jego uogólnieniem na wyższe wymiary jest sfera jednostkowa. Do zdefiniowania innych „okręgów jednostkowych”, np. okręgu Riemanna, można skorzystać z innych pojęć „odległości” (zob. przestrzeń unormowana).
Równania
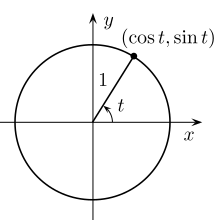
[edytuj | edytuj kod]Jeżeli jest punktem okręgu jednostkowego leżącym w pierwszej ćwiartce, to i są długościami przyprostokątnych trójkąta prostokątnego o przeciwprostokątnej długości 1. Z twierdzenia Pitagorasa oraz spełniają równanie:
Ponieważ dla każdego a odbicie dowolnego punktu leżącego na okręgu jednostkowych względem osi rzędnych bądź odciętych nadal leży na tym okręgu, to powyższe równanie jest spełnione dla wszystkich punktów leżących na okręgu jednostkowym, a nie tylko tych z pierwszej ćwiartki.
Okrąg jednostkowy można zadać wielorako. Korzystając z własności liczb zespolonych uzyskuje się charakteryzację:
- wykładniczą
- trygonometryczną
Funkcje trygonometryczne
[edytuj | edytuj kod]
Na okręgu jednostkowym można zdefiniować funkcje trygonometryczne sinusa i cosinusa: jeżeli jest punktem okręgu jednostkowego, a promień o początku w i końcu w tworzy kąt z dodatnią półosią (przy czym mierzy się go przeciwnie do ruchu wskazówek zegara zaczynając od osi), to:
Równanie daje wtedy zależność:
(Zapis jest zwyczajową formą zapisu potęg dla wszystkich funkcji trygonometrycznych).
Okrąg jednostkowy daje intuicyjny wgląd w okresowość wspomnianych funkcji:
dla dowolnej liczby całkowitej

Wyżej wymienione tożsamości można podsumować następująco: współrzędne punktu na okręgu jednostkowym nie ulegają zmianie przy zwiększeniu bądź zmniejszeniu kąta o dowolną liczbę obrotów (1 obrót = 2п radianów = 360°).
Definiowane z elementów trójkąta prostokątnego sinus, cosinus oraz inne funkcje trygonometryczne są określone tylko dla miar kątów większych od i mniejszych od Zdefiniowane za pomocą okręgu jednostkowego mają one swoje sensowne, intuicyjne uogólnienia dla dowolnej rzeczywistej miary kąta, co pokazano na rysunku obok.
Dynamika zespolona
[edytuj | edytuj kod]
Zbiór Julii dyskretnego nieliniowego układu dynamicznego z funkcją ewolucji:
jest okręgiem jednostkowym. Jest to najprostszy przypadek i z tego powodu jest on szeroko stosowany w badaniach nad układami dynamicznymi.
Zobacz też
[edytuj | edytuj kod]Przypisy
[edytuj | edytuj kod]- ↑
 Szymon Charzyński, Okrąg jednostkowy i definicje funkcji trygonometrycznych, kanał Khan Academy na YouTube, 12 listopada 2013 [dostęp 2024-10-24].
Szymon Charzyński, Okrąg jednostkowy i definicje funkcji trygonometrycznych, kanał Khan Academy na YouTube, 12 listopada 2013 [dostęp 2024-10-24].
- ↑ Eric W. Weisstein, Unit Circle, [w:] MathWorld, Wolfram Research (ang.). [dostęp 2024-10-24].
- ↑
 Filip Turoboś, Funkcje trygonometryczne kąta, na końcowym ramieniu którego znajduje się punkt o danych współrzędnych, Zintegrowana Platforma Edukacyjna – Ministerstwo Edukacji Narodowej, zpe.gov.pl [dostęp 2024-10-24].
Filip Turoboś, Funkcje trygonometryczne kąta, na końcowym ramieniu którego znajduje się punkt o danych współrzędnych, Zintegrowana Platforma Edukacyjna – Ministerstwo Edukacji Narodowej, zpe.gov.pl [dostęp 2024-10-24].
- ↑ a b dualność, [w:] Encyklopedia PWN [online], Wydawnictwo Naukowe PWN [dostęp 2024-10-24].
- ↑ zbiór Julii, [w:] Encyklopedia PWN [online], Wydawnictwo Naukowe PWN [dostęp 2024-10-24].

