Saltar para o conteúdo

Árvore splay

Origem: Wikipédia, a enciclopédia livre.
Árvore splay
Tipo Árvore
Ano 1985
Inventado por Daniel Sleator e Robert Tarjan
Complexidade de Tempo em Notação big O
Algoritimo Caso Médio Pior Caso
Espaço
Busca amortizado
Inserção amortizado
Remoção amortizado

Uma árvore splay é uma árvore binária de busca autoajustável, com a propriedade adicional de tornar os elementos recentemente acessados, fáceis de acesso novamente, pois os mantém em sua raiz. Suas operações básicas, como remoção e inserção, são executadas em O(log n). Todas as suas operações colocam o elemento envolvido na operação na raiz, através de rotações. Para muitas sequências de operações não aleatórias, as árvores splay têm melhor desempenho do que outras árvores de busca, mesmo quando o padrão específico da sequência é desconhecido. A árvore splay foi inventada por Daniel Sleator e Robert Tarjan em 1985.[1]

Vantagens

[editar | editar código-fonte]

O bom desempenho para uma árvore de splay depende do fato de que é autoajustável, na medida em que os nós com acesso frequente se moverão mais próximos da raiz onde eles podem ser acessados mais rapidamente. A altura do pior caso - embora improvável - é O (n), sendo a média O (log n ).

As vantagens incluem:

  • Desempenho comparável: O desempenho médio do caso é tão eficiente quanto outras árvores.[2]
  • Fácil de implementar;

Desvantagens

[editar | editar código-fonte]

A desvantagem mais significativa é que a altura de uma árvore splay pode ser linear. Por exemplo, este será o caso depois de acessar todos os elementos n em ordem não decrescente. Uma vez que a altura de uma árvore corresponde ao pior caso de tempo de acesso, isso significa que o custo real de uma operação pode ser alto. No entanto, o custo de acesso deste pior caso é, O (log n ). Além disso, o custo de acesso esperado pode ser reduzido a O (log n ) usando uma variante aleatória.[3]

O pior caso ocorre quando os nodos da árvore são acessados sequencialmente em ordem. Isto deixa a árvore completamente desbalanceada.

A representação de árvores de splay pode mudar mesmo quando elas são acessadas de forma "somente leitura" (isto é, por operações de "pesquisa"). Isto complica o uso de tais em um ambiente multi-threaded. Especificamente, gerenciamento extra é necessário se vários segmentos são autorizados a executar operações de pesquisa simultaneamente. Isso também os torna inadequados para uso geral em programação puramente funcional, embora mesmo lá eles possam ser usados ​​de maneiras limitadas para implementar filas de prioridade.

Operações

[editar | editar código-fonte]

Splay

[editar | editar código-fonte]

Quando um nó n é acessado, uma operação de splay é executada em n para movê-lo para a raiz. Para executar uma operação de splay, realizamos uma sequência de rotações, cada um dos quais move n mais próximo da raiz. Ao executar uma operação de splay no nó de interesse após cada acesso, os nós recentemente acessados são mantidos perto da raiz e a árvore permanece aproximadamente equilibrada.

Rotação simples (ZIG)

[editar | editar código-fonte]
  • ZIG (Rotação para Direita) e ZAG (Rotação para Esquerda)
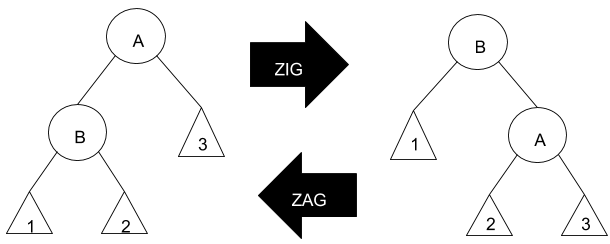
Rotações ZIG e ZAG
Rotações ZIG e ZAG

Se pai(B) é raiz fazemos apenas uma rotação para esquerda ou direita.

Rotação dupla (ZIG-ZIG, ZAG-ZAG)

[editar | editar código-fonte]
  • ZIG-ZIG e ZAG-ZAG:

Se pai(C) não é raiz e C e pai(C) são filhos do mesmo lado, fazemos duas rotações para direita ou duas rotações para a esquerda, no mesmo sentido começando pelo pai(pai(C)).

Rotação dupla ZIG-ZAG

[editar | editar código-fonte]
  • ZIG-ZAG:

Se pai(C) não é raiz e C e pai(C) são filhos do lado oposto, faz uma rotação em pai(C) para direita e outra rotação no avô para esquerda de C.

Rotação dupla ZAG-ZIG

[editar | editar código-fonte]
  • ZAG-ZIG:

Se pai(C) não é raiz e C e pai(C) são filhos do lado oposto, faz uma rotação em pai(C) para esquerda e outra rotação no avô para direita de C.

Busca

[editar | editar código-fonte]

Como a Splay Tree é um algoritmo, que ao passar das operações ela vai se balanceando, inicia na raiz da árvore t procurando pelo item i, se a busca encontra um nodo x que contenha i, o nodo x é splayed.Se a busca não encontra i, último nodo não nulo da árvore é splayed e um ponteiro nulo é retornado 

struct node *splay(struct node *root, int key)
{
    // Base cases: root is NULL or key is present at root
    if (root == NULL || root→key == key)
        return root;

    // Key lies in left subtree
    if (root→key > key)
    {
        // Key is not in tree, we are done
        if (root→left == NULL) return root;

        // Zig-Zig (Left Left)
        if (root→left→key > key)
        {
            // First recursively bring the key as root of left-left
            root→left→left = splay(root→left→left, key);

            // Do first rotation for root, second rotation is done after else
            root = rightRotate(root);
        }
        else if (root→left→key < key) // Zig-Zag (Left Right)
        {
            // First recursively bring the key as root of left-right
            root→left→right = splay(root→left→right, key);

            // Do first rotation for root→left
            if (root→left→right != NULL)
                root→left = leftRotate(root→left);
        }

        // Do second rotation for root
        return (root→left == NULL)? root: rightRotate(root);
    }
    else // Key lies in right subtree
    {
        // Key is not in tree, we are done
        if (root→right == NULL) return root;

        // Zag-Zig (Right Left)
        if (root→right→key > key)
        {
            // Bring the key as root of right-left
            root→right→left = splay(root→right→left, key);

            // Do first rotation for root→right
            if (root→right→left != NULL)
                root→right = rightRotate(root→right);
        }
        else if (root→right→key < key)// Zag-Zag (Right Right)
        {
            // Bring the key as root of right-right and do first rotation
            root→right→right = splay(root→right→right, key);
            root = leftRotate(root);
        }

        // Do second rotation for root
        return (root→right == NULL)? root: leftRotate(root);
    }
}

// The search function for Splay tree.  Note that this function
// returns the new root of Splay Tree.  If key is present in tree
// then, it is moved to root.
struct node *search(struct node *root, int key)
{
    return splay(root, key);
}

Inserção

[editar | editar código-fonte]

A inserção na Splay tree é parecida com a que ocorre nas Árvores Binarias de Pesquisa - BST -, apenas com uma adição que o elemento que foi adicionado se torna a nova raiz. 

struct node *insert(struct node *root, int k)
{
    // Simple Case: If tree is empty
    if (root == NULL) return newNode(k);

    // Bring the closest leaf node to root
    root = splay(root, k);

    // If key is already present, then return
    if (root→key == k) return root;

    // Otherwise allocate memory for new node
    struct node *newnode  = newNode(k);

    // If root's key is greater, make root as right child
    // of newnode and copy the left child of root to newnode
    if (root→key > k)
    {
        newnode→right = root;
        newnode→left = root→left;
        root→left = NULL;
    }

    // If root's key is smaller, make root as left child
    // of newnode and copy the right child of root to newnode
    else
    {
        newnode→left = root;
        newnode→right = root→right;
        root→right = NULL;
    }

    return newnode; // newnode becomes new root
}

Bibliografia

[editar | editar código-fonte]

Referências

  1. ↑ Sleator & Tarjan 1985.
  2. ↑ Goodrich , Tamassia & Goldwasser 2014
  3. ↑ Albers & Karpinski 2002.
Obtida de "https://pt.wikipedia.org/w/index.php?title=Árvore_splay&oldid=55333354"