Пређи на садржај

Polarizovana svetlost

С Википедије, слободне енциклопедије
Turmalini.
U prirodnoj svetlosti oscilacije su normalne na smer širenja, to jest na zrake u različitim ravninama. Zato se takva svetlost zove nepolarizovana svetlost.
Kad se dve pločice od turmalina postave jedna prema drugoj, prozirnost zavisi od njihovog međusobnog položaja.
Turmalinska pločica se može zamisliti kao mehanička mrežica koja od svih oscilacija propušta samo onu komponentu koja leži u izvesnoj ravnini. Takva svetlost kod koje se oscilovanje zbiva samo u jednoj ravni zove se polarizovana svetlost.
Prema Brusterovom pravilu prelomljeni zrak (refrakcija) potpuno je pravolinijski polarizovan ako svetlost pada na ravnu površinu pod takvim uglom da su odbijeni (reflektovana) i prelomljeni zrak normalni..[1][2]
Polarizacija svetlosti refleksijom.
Oscilovanje upadnog zraka može biti u ravni upadanja ili normalno na nju.
Rejlijevo rasejanje[3] je jače nakon zalaska Sunca.

Polarizovana svetlost je ona vrsta svetlosti kod koje elektromagnetni talasi osciluju samo u jednoj ravni.[4] Ta ravan je normalna na smer širenja zračenja.[4] Polarizacijom svetlosti pokazuje se talasna priroda svetlosti i to da je svetlost transverzalni talas.[5] U prirodi svetlost je nepolarizirana, odnosno sa istom verovatnoćom vektori električnog polja (E) i magnetnog polja (B) zauzimaju bilo koji smer normalan na vektor kretanja svetlosti.[5] Kada dođe do loma odnosno refleksije svetla, nastaje polarizovana svetlost.[5]

Polarizacija svetlosti je pojava nesimetričnog oscilovanja električnog i magnetnog polja koje šireći se čini svetlost. Nastaje međudelovanjem svetlosti i materije: refleksijom, dvolomom ili raspršenjem. Svetlost je linearno polarizirana ako električno polje stalno osciluje u istoj ravni, kružno polarizovana ako se ravan oscilovanja električnog polja jednoliko vrti (u smeru kazaljke na satu ili u suprotnom smeru), delimično polarizovana ako oscilovanje električnog polja nije jednakih amplituda u svim ravnima, te nepolarizovana ako električno polje jednako osciluje u svim ravninama normalnim na smer širenja svetlosti.[6]

Polarizacija je svojstvo koje se odnosi na transverzalne talase koje specificira geometrijsku orijentaciju oscilacija.[7][8][9][10][11] U transverzalnom talasu, pravac oscilacije je normalan na pravac kretanja talasa.[10] Jednostavan primer polarizovanog transverzalnog talasa su vibracije koje putuju duž zapetog užeta; na primer, u muzičkom instrumentu kao što je struna gitare. U zavisnosti od toga kako se žica okine, vibracije se mogu kretati u vertikalnom pravcu, horizontalnom pravcu, ili pod bilo kojim uglom normalnim na žicu. Za razliku od toga kod longitudinalnih talasa, kao što su zvučni talasi u tečnosti ili gasu, pomicanje čestica u oscilaciji uvek je u pravcu propagacije, tako da talasi ne manifestuju polarizaciju. Transverzalni talasi koji ispoljavaju polarizaciju su elektromagnetni talasi kao što je svetlo ili radio talasi, gravitacioni talasi,[12] i transverzalni zvučni talasi (S talasi) u čvrstim materijalima. U nekim tipovima transverzalnih talasa, pomeranje talasa je ograničeno na jedan pravac, tako da oni takođe ne pokazuju polarizaciju; na primer, kod površinskih talasa u tečnostima (gravitacioni talasi), talasno pomeranje čestica je uvek u vertikalnoj ravni.

Prema kvantnoj mehanici, elektromagnetni talasi se mogu smatrati strujama čestica zvanih fotoni. Kad se gledaju na taj način, polarizacija elektromagnetnog talasa je određena kvantno mehaničkim svojstvom fotona koje se naziva njihovim spinom.[13][14] Foton ima jedan od dva moguća spina: on se može okretati bilo u smislu desne ruke ili u smislu leve ruke oko svog pravca putovanja. Kružno polarizovani elektromagnetni talasi se sastoje od fotona sa samo jednim tipom spina, bilo desnoruki ili levoruki. Linearno polarizovani talasi se sastoje od fotona koji su u superpoziciji desno i levo kružno polarizovanih stanja, sa jednakom amplitudom i fazama sinhronizovanim da daju oscilacije u ravni.[14]

Polarizacija svetlosti pomoću kristala

[уреди | уреди извор]

Pojave interferencije i difrakcije svetlosti potvrđuju da je svetlost talasne prirode. Međutim, iz njih se ne dobija odgovor da li je svetlost longitudinalno ili transverzalno talasno kretanje. Na to pitanje daje odgovor polarizacija svetlosti.

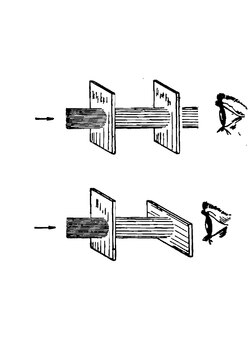
Uzmimo dve pločice kristala turmalina koje su brušene paralelno s glavnom kristalnom osom. Svaka pločica za sebe propušta svetlost kako se god postavi. Postave li se obe pločice turmalina jedna prema drugoj, prozirnost će zavisiti od njihovog međusobnog položaja. Svetlost će najjače prolaziti kada su kristalne ose obe ploče međusobno paralelne. Zakretanjem jedne ploče prema drugoj prolaziće sve manje svetlosti, a kod normalnog položaja dve kristalne ose ploče će biti neprozirne. Iz toga izlazi da prva pločica menja svojstva zraka svetlosti koji kroz nju prolazi tako da zrak svetlosti ima različita svojstva u smerovima normalnim na pravac kretanja svetlosti. Ta pojavu se naziva polarizacijom svetlosti.

Iz pojave polarizacije svetlosti nužno izlazi da su talasi svetlosti transverzalni, to jest da se oscilovanje zbiva normalno na smer širenja zraka svetlosti. Kod longitudinalnih talasa, na primer kod talasa zvuka ne može u vazduhu biti nikakve razlike u bilo kojem smeru, normalnom na smer širenja zvuka. U prirodnoj svetlosti oscilacije su normalne na smer širenja, to jest na zraku u različitim ravninama. Zato se takvu svetlost zoviva nepolarizovana svetlost.

Turmalinska pločica se može zamisliti da je mehaničku mrežica koja od svih oscilacija propušta samo onu komponentu koja leži u izvesnoj ravni. Takva se svetlost kod koje se oscilovanje zbiva samo u jednoj ravni zove se polarizovana svetlost. Naprava (u našem slučaju prva pločica), koja prirodnu svetlost pretvara u polarizovanu, zove se polarizator. Kako je svetlost koja je izašla iz turmalinske pločice polarizovana, ona će ona proći kroz drugu pločicu samo ako su im kristalne ose paralelne. Kod normalnih osa svetlost neće moći da prođe, i pločice će biti neprozirne. Kod ostalih položaja pločica, to jest kod zakreta za bilo koji ugao manji od 90°, prolaziće samo jedan mali deo, to jest jedna komponenta polarizovane svetlosti. Druga pločica koja je isto polarizator pomoću koje se može odrediti da li je svetlost polarizovana ili nije zove se analizator.

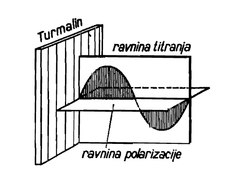
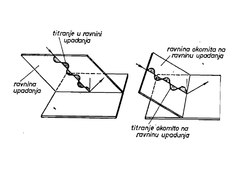
Iz dosadašnjeg razmatranja može se reći da je polarizacija svetlosti oscilovanje svetlosti samo u jednoj ravni koja se zove ravan oscilovanja. To je linearno polarizovana svetlost. Ravan položena kroz zrak normalno na ravan oscilovanja zove se ravan polarizacije. Polarizacija svetlosti kod prolaza kroz turmalin i druge kristale tumači se rasporedom molekula u kristalu koji propuštaju oscilacije samo u jednoj ravni.[15]

Polarizacija svetlosti dvolomom

[уреди | уреди извор]
Glavni članak: Dvolom

Polarizacija svetlosti dvolomom nastaje pri prolasku svetlosti kroz neke anizotropne kristale (na primer kalcit, kvarc) u kojima se, osim redovnog lomljenog zraka koji se podvrgava Snelovom zakonu prelamanja, pojavljuje još i izvanredan zrak, koja se lomi pod drukčijim uglom. Ta su dva zraka linearno polarizovana u međusobno normalnim smerovima.

Polarizacija svetlosti refleksijom

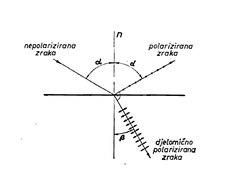
[уреди | уреди извор]

Polarizacija svetlosti refleksijom nastaje pri upadu zraka svetlosti na granicu optičkih sredstava, gde svetlost delimično prolazi prelamajući se, a delimično se reflektuje (odbija). Reflektovani i prelomljeni snopovi delimično su polarizovani tako da su im ravni polarizacije međusobno normalne. Ravan polarizacije reflektovane svetlosti normalna je na ravan refleksije, dok je ravan polarizacije prelomljene svetlosti u ravni refleksije, odnosno loma. Ako reflektovan i prelomljen zrak zatvaraju pravi ugao, dolazi do potpune, linearne polarizacije. Tada ugao upadnog zraka svetlosti α zadovoljava Brusterovo pravilo:

gde su n1 i n2 indeksi loma sredstava.

Objašnjenje

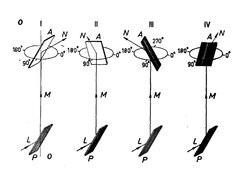
[уреди | уреди извор]

Ako se uzme da zrak svetlosti L upada pod uglom od 57° na staklenu pločicu P, koja je sa stražnje strane premazana crnom bojom tako, da ne bi smetala prolazna svetlost. Ploča P je tako nagnuta, da od nje reflektovan (odbijen) zrak M ide normalno prema gore. Reflektovan zrak M upada na staklenu pločicu A, koja je paralelna sa pločom P, dakle pod istim uglom od 57°. Ako se okrene staklena ploča A oko ose OO, to jest oko reflektovanog zraka M kao ose, vidi se da je jačina (intenzitet) reflektovanog zraka N od ploče A (koja se pušta da padne na jedan zaslon) menja, to će biti sve manji, a kad se ploču A zakrene za 90°, to jest kada ploča A dođe u položaj II reflektovani zrak N će nestati. Ako se ploču A dalje okreće, opet će se pojaviti reflektovani zrak N, te će mu jačina rasti sve dotle, dok se ploču A ne zakrene za 180°, to jest u položaj III, kada će mu jačina biti najveća. Daljim zakretanjem ploče A jačina zraka N ponovno će opadati, a kod zaokreta za 270°, to jest u položaju IV reflektovani zrak će nestati. Dakle jačina reflektovanog zraka N biće najveća kad se ravan upadanja (refleksije) na obe staklene ploče podudaraju (prvi i treći položaj). Za svaki drugi položaj ploče A prema ploči P jačina reflektovanog zraka N biće slabija, a u položaju, kad su ravni refleksije na obe staklene ploče međusobno normalne, zrak N će nestati (drugi i četvrti položaj). Ta pojava nastaje zbog polarizacije svetlosti. Znači da reflektirani zrak M nema ista svojstva kao zrak L. Kad bi zrak M bio longitudinalni talas, jačina reflektovanog zraka N ne bi zavisila od položaja ploče A. Međutim kod transverzalnog talasa to je važno. Kod transverzalnog talasa postoje dva karakteristična smera oscilovanja s obzirom na ravan upadanja (refleksije), to jest na ravan u kojoj se nalazi upadajući i reflektovani zrak. Oscilovanje upadajućeg zraka može biti u ravni upadanja ili normalno na tu ravninu. Iz toga sledi da će od smera oscilovanja zavisiti, da li će zrak lakše prodreti u staklo ili će se reflektovati. U položaju I i III je reflektovani zrak N totalno (potpuno) polarizovan, a njegova ravan polarizacije je ravan upadanja, to jest raflektovana svetlost osciluje normalno na ravan upadanja.

Polarizacija svetlosti apsorpcijom

[уреди | уреди извор]

Polarizacija svetlosti apsorpcijom nastaje pri prolasku svetlosti kroz materiju koja propušta svetlost samo određene polarizacije. U dikroitičnim dvolomnim kristalima (na primer turmalin) jedan se zrak apsorbuje, a propušteni se zrak polarizuje. Svetlosna jačina propuštene svetlosti jednaka je polovini svetlosne jačine upadne nepolarizovane svetlosti.

Polarizacija svetlosti u atmosferi

[уреди | уреди извор]

Polarizacija svetlosti u atmosferi nastaje raspršenjem svetlosti na česticama vazduha. Područje najjače polarizacije nalazi se pod uglom od 90° u odnosu na Sunce, na primer kada je Sunce na horizontu, najjače je polarizovana nebeska svetlost blizu horizonta).

Reference

[уреди | уреди извор]
  1. ^ David Brewster (1815) "On the laws which regulate the polarisation of light by reflection from transparent bodies," Philosophical Transactions of the Royal Society of London, 105: 125-159.
  2. ^ Lakhtakia, Akhlesh (jun 1989). „Would Brewster recognize today's Brewster angle?” (PDF). Optics News. OSA. 15 (6): 14—18. doi:10.1364/ON.15.6.000014. 
  3. ^ Young, Andrew T (1981). „Rayleigh scattering”. Applied Optics. 20 (4): 533—5. Bibcode:1981ApOpt..20..533Y. PMID 20309152. doi:10.1364/AO.20.000533. 
  4. ^ а б Generalić, Eni. "Polarizirana svetlost." Englesko-hrvatski kemijski rječnik & glosar. 31 July 2014. KTF-Split. 14. siječnja 2015. <http://glossary.periodni.com>.
  5. ^ а б в Zlonoga, Hana. „Polarizacija svetlosti”. Uporaba računala u nastavi. PMF Zagreb. Архивирано из оригинала 9. 2. 2015. г. Приступљено 14. 1. 2015. 
  6. ^ Polarizacija, "Hrvatska enciklopedija", Leksikografski zavod Miroslav Krleža, www.enciklopedija.hr, 2016.
  7. ^ Shipman, James; Wilson, Jerry D.; Higgins, Charles A. (2015). An Introduction to Physical Science, 14th Ed. Cengage Learning. стр. 187. ISBN 1305544676. 
  8. ^ Muncaster, Roger (1993). A-level Physics. Nelson Thornes. стр. 465—467. ISBN 0748715843. 
  9. ^ Singh, Devraj (2015). Fundamentals of Optics, 2nd Ed. PHI Learning Pvt. Ltd. стр. 453. ISBN 8120351460. 
  10. ^ а б Avadhanulu, M. N. (1992). A Textbook of Engineering Physics. S. Chand Publishing. стр. 198—199. ISBN 8121908175. 
  11. ^ Desmarais, Louis (1997). Applied Electro Optics. Pearson Education. стр. 162—163. ISBN 0132441829. 
  12. ^ Le Tiec, A.; Novak, J. (jul 2016). „Theory of Gravitational Waves”. arXiv:1607.04202 Слободан приступ. doi:10.1142/9789813141766_0001. 
  13. ^ Lipson, Stephen G.; Lipson, Henry; Tannhauser, David Stefan (1995). Optical Physics. Cambridge University Press. стр. 125—127. ISBN 9780521436311. 
  14. ^ а б Waldman, Gary (2002). Introduction to Light: The Physics of Light, Vision, and Color. Courier Corporation. стр. 79—80. ISBN 9780486421186. 
  15. ^ Velimir Kruz: "Tehnička fizika za tehničke škole", "Školska knjiga" Zagreb, 1969.

Literatura

[уреди | уреди извор]
  • Principles of Optics, , M. Born & E. Wolf, Cambridge University. (7th изд.). 1999. ISBN 978-0-521-64222-4. .
  • Fundamentals of polarized light: a statistical optics approach, C. Brosseau, Wiley. 1998. ISBN 978-0-471-14302-4..
  • Polarized Light, second edition, Dennis Goldstein, Marcel Dekker. 2003. ISBN 978-0-8247-4053-5.
  • Field Guide to Polarization, Edward Collett, SPIE Field Guides vol. FG05, SPIE. 2005. ISBN 978-0-8194-5868-1..
  • Polarization Optics in Telecommunications, Jay N. Damask, Springer. 2004. ISBN 978-0-387-22493-0..
  • Polarized Light in Nature, G. P. Können, Translated by G. A. Beerling, Cambridge University. 1985. ISBN 978-0-521-25862-3..
  • Polarised Light in Science and Nature, D. Pye, Institute of Physics. 2001. ISBN 978-0-7503-0673-7..
  • Polarized Light, Production and Use, William A. Shurcliff, Harvard University, 1962.
  • Ellipsometry and Polarized Light, R. M. A. Azzam and N. M. Bashara, North-Holland. 1977. ISBN 978-0-444-87016-2.
  • Secrets of the Viking Navigators—How the Vikings used their amazing sunstones and other techniques to cross the open oceans, Leif Karlsen, One Earth Press, 2003.

Spoljašnje veze

[уреди | уреди извор]
Polarizovana svetlost на Викимедијиној остави.
Преузето из „https://sr.wikipedia.org/w/index.php?title=Polarizovana_svetlost&oldid=28524133”