Không gian tích trong

Biểu diễn hình học của góc giữa hai vectơ, được định nghĩa bởi tích trong.

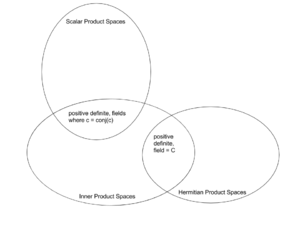
Scalar product spaces, inner product spaces, Hermitian product spaces. — Các không gian tích vô hướng trên một trường bất kỳ có trang bị các "tích vô hướng" đối xứng và tuyến tính với đối số thứ nhất. Không gian tích Hermite được giới hạn trong trường số phức và có "tích Hermite" đối xứng liên hợp và tuyến tính với đối số thứ nhất. Không gian tích trong có thể được định nghĩa trên một trường bất kỳ và có các "tích trong" tuyến tính với đối số thứ nhất, đối xứng liên hợp và xác định dương. Không giống như các tích trong, tích vô hướng và tích Hermite không nhất thiết phải có tính xác định dương.

Trong toán học, một không gian tích trong hay không gian Hausdorff tiền Hilbert^[1]^[2] là một không gian vectơ được trang bị một phép toán hai ngôi gọi là tích trong. Phép toán này liên kết mỗi cặp vectơ trong không gian với một đại lượng vô hướng gọi là tích trong của các vectơ, thường được ký hiệu bởi dấu bra-ket (ví dụ $\langle a,b\rangle$ .)^[3] Tích trong cho phép định nghĩa các khái niệm trực quan hình học như độ dài của một vectơ hay góc giữa hai vectơ. Chúng cũng cung cấp các cách định nghĩa tính trực giao giữa hai vectơ (tích trong bằng 0). Không gian tích trong tổng quát hóa không gian Euclid (trong đó tích trong chính là tích vô hướng^[4]) cho các không gian vectơ với số chiều bất kỳ (có thể vô hạn), và được nghiên cứu trong giải tích hàm. Không gian tích trong trên trường số phức đôi khi được gọi là không gian unita. Khái niệm không gian vectơ với một tích trong lần đầu tiên được sử dụng bởi Giuseppe Peano, vào năm 1898.^[5]

Một không gian tích trong thường tạo ra một chuẩn liên hệ với nó, (trong ảnh, |x| và |y| là các chuẩn của $x$ và $y$ ), một cách chính tắc nó làm cho mọi không gian tích trong là không gian vectơ định chuẩn. Nếu không gian định chuẩn này cũng là một không gian Banach thì không gian tích trong được gọi là không gian Hilbert.^[1] Nếu một không gian tích trong $(H, ⟨\cdot, \cdot⟩)$ không là không gian Hilbert thì nó có thể được "bổ sung" để trở thành không gian Hilbert $(H, ⟨\cdot, \cdot⟩ H)$ , gọi là làm đầy đủ hóa. Nói một cách rõ ràng, điều này nghĩa là $H$ được nhúng tuyến tính và đẳng cự vào một không gian con trù mật của $H$ và sao cho tích trong $⟨\cdot, \cdot⟩ H$ trên $H$ là sự bổ sung liên tục của không gian tích trong ban đầu $⟨\cdot, \cdot⟩$ .^[1]^[6]

Định nghĩa

Trong bài này, trường vô hướng, ký hiệu $𝔽$ là trường số thực $\mathbb {R}$ hoặc trường số phức $\mathbb {C}$ .

Không gian tích trong, một cách chính thức là một không gian vectơ $V$ trên trường $𝔽$ cùng với một ánh xạ

\langle \cdot ,\cdot \rangle :V\times V\to \mathbb {F}

gọi là một tích trong nếu nó thỏa mãn các điều kiện tiên đề (1), (2), và (3) sau đây^[1] đối với mọi vectơ $x, y, z \in V$ và mọi vô hướng $a \in 𝔽$ :^[7]^[8]^[9]

Tuyến tính đối với đối số thứ nhất^{[note 1]}
${\begin{aligned}\langle ax,y\rangle &=a\langle x,y\rangle \\\langle x+y,z\rangle &=\langle x,z\rangle +\langle y,z\rangle \end{aligned}}$
- Nếu điều kiện (1) được thỏa mãn và nếu tích $\langle \cdot ,\cdot \rangle$ cũng là phản tuyến tính (còn gọi là tuyến tính liên hợp) đối với đối số thứ hai^{[note 2]} thì $\langle \cdot ,\cdot \rangle$ được gọi là dạng nửa tuyến tính (sesquilinear form).^[1]
Đối xứng liên hợp hay đối xứng Hermite:^{[note 3]}
$\langle x,y\rangle ={\overline {\langle y,x\rangle }}$
- Điều kiện (1) và (2) là các tính chất định nghĩa một dạng Hermite, là một loại đặc biệt của dạng nửa tuyến tính.^[1] Một dạng nửa tuyến tính là Hermite khi và chỉ khi $\langle x,x\rangle$ là thực với mọi $x$ .^[1] Cụ thể, từ điều kiện (2) suy ra rằng^{[note 4]} $\langle x,x\rangle$ là một số thực với mọi $x$ .
Tính xác định dương:^[1]
$\langle x,x\rangle >0,\quad {\text{ nếu }}x\neq 0.$

Ba điều kiện trên là các tính chất định nghĩa một tích trong, đó là lý do tại sao tích trong đôi khi được định nghĩa (một cách tương đương) là một dạng Hermite xác định dương. Một tích trong có thể được định nghĩa một cách tương đương là một dạng nửa tuyến tính xác định dương.^[1]^{[note 5]}

Giả thiết rằng (1) được thỏa mãn, điều kiện (3) cũng sẽ được thỏa mãn khi và chỉ khi hai điều kiện thêm (4) và (5) dưới đây được thỏa mãn:^[6]^[1]

Tính nửa xác định dương hay xác định không âm:^[1]
$\langle x,x\rangle \geq 0$
- Các điều kiện (1), (2), và (4) là các tính chất định nghĩa một dạng Hermite nửa xác định dương, cho phép ta định nghĩa một nửa chuẩn trên $V$ được cho bởi $v \mapsto \sqrt ⟨ v, v ⟩$ . Nửa chuẩn này là một chuẩn khi và chỉ khi điều kiện (5) được thỏa mãn.
Tính tách điểm hay xác định:
$\langle x,x\rangle =0\quad {\text{ suy ra }}\quad x=0.$

Các điều kiện (1) đến (5) được thỏa mãn bởi mọi tích trong.

Tính chất sơ cấp

Tính xác định dương và tuyến tính tương ứng đảm bảo rằng:

{\begin{aligned}\langle x,x\rangle &=0\Rightarrow x=\mathbf {0} \\\langle \mathbf {0} ,x\rangle &=\langle 0x,x\rangle =0\langle x,x\rangle =0\end{aligned}}

Từ tính đối xứng liên hợp suy ra $⟨ x, x ⟩$ là thực với mọi $x$ , bởi vì

\langle x,x\rangle ={\overline {\langle x,x\rangle }}\,.

Tính đối xứng liên hợp và tuyến tính đối với đối số thứ nhất dẫn đến

{\begin{aligned}\langle x,ay\rangle &={\overline {\langle ay,x\rangle }}={\overline {a}}{\overline {\langle y,x\rangle }}={\overline {a}}\langle x,y\rangle \\\langle x,y+z\rangle &={\overline {\langle y+z,x\rangle }}={\overline {\langle y,x\rangle }}+{\overline {\langle z,x\rangle }}=\langle x,y\rangle +\langle x,z\rangle \,\end{aligned}}

đây tức là tính tuyến tính liên hợp đối với đối số thứ hai. Vì vậy, một không gian tích trong là một dạng nửa tuyến tính.

Có thể suy ra tổng quát hóa sau đây của khai triển bình phương của tổng:

\langle x+y,x+y\rangle =\langle x,x\rangle +\langle x,y\rangle +\langle y,x\rangle +\langle y,y\rangle \,.

Các tính chất sau đây hợp thành tính tuyến tính đối với đối số thứ nhất và thứ hai:

{\begin{aligned}\langle x+y,z\rangle &=\langle x,z\rangle +\langle y,z\rangle \,,\\\langle x,y+z\rangle &=\langle x,y\rangle +\langle x,z\rangle \end{aligned}}

còn được gọi là tính cộng.

Với trường hợp $\mathbb {F} =\mathbb {R} ,$ tính đối xứng liên hợp được đơn giản về tính đối xứng, còn tính nửa tuyến tính trở thành tính song tuyến. Vì thế một tích trong trên một không gian vectơ thực là một dạng song tuyến tính đối xứng xác định dương. Tức là,

{\begin{aligned}\langle x,y\rangle &=\langle y,x\rangle \\\Rightarrow \langle -x,x\rangle &=\langle x,-x\rangle \,,\end{aligned}}

và khai triển nhị thức trở thành:

\langle x+y,x+y\rangle =\langle x,x\rangle +2\langle x,y\rangle +\langle y,y\rangle \,.

Định nghĩa, ký hiệu khác và chú thích

Một trường hợp đặc biệt thường gặp của tích trong là tích vô hướng của hai vectơ, thường được ký hiệu bởi dấu chấm ở giữa $a\cdot b.$

Một số tác giả, đặc biệt trong lĩnh vực vật lý và đại số ma trận thường định nghĩa tích trong và dạng nửa tuyến tính nhưng với tính tuyến tính của nó là ở đối số thứ hai thay vì thứ nhất. Vậy đối số thứ nhất có tính tuyến tính liên hợp thay vì thứ hai. Trong các ngành này chúng ta thường viết tích trong $\langle x,y\rangle$ là $\langle y\mid x\rangle$ (ký hiệu bra-ket của cơ học lượng tử), tương ứng là $y † x$ (tích vô hướng với quy ước lập tích ma trận $AB$ , lấy hàng của $A$ nhân cột của $B$ ).

Một số ví dụ

Số thực

Ví dụ đơn giản nhất là các số thực với tích thông thường giữa các số là tích trong^[4]

\langle x,y\rangle =xy.

Không gian vectơ Euclid

Tổng quát, không gian thực $n$ chiều $\mathbb {R} ^{n}$ với tích vô hướng là một không gian tích trong,^[4] là một ví dụ của không gian vectơ Euclid.

\left\langle {\begin{bmatrix}x_{1}\\\vdots \\x_{n}\end{bmatrix}},{\begin{bmatrix}y_{1}\\\vdots \\y_{n}\end{bmatrix}}\right\rangle =x^{\textsf {T}}y=\sum _{i=1}^{n}x_{i}y_{i}=x_{1}y_{1}+\cdots +x_{n}y_{n},

trong đó $x T$ là chuyển vị của $x$ .

Không gian tọa độ phức

Dạng tổng quát của một tích trong trên $\mathbb {C} ^{n}$ được gọi là dạng Hermite và được cho bởi

\langle x,y\rangle =y^{\dagger }\mathbf {M} x={\overline {x^{\dagger }\mathbf {M} y}},

trong đó $M$ là một ma trận Hermite nửa xác định dương và $y †$ là chuyển vị liên hợp của $y$ .

Tích trong phức thường gặp nhất là tích vô hướng chính tắc phức, trong đó ma trận $M$ được chọn là ma trận đơn vị.

Không gian Hilbert

Bài viết về không gian Hilbert có một số ví dụ về không gian tích trong, trong đó metric được tạo bởi tích trong tạo ra không gian metric đầy đủ. Một ví dụ của không gian tích trong tạo ra một metric không đầy đủ là không gian $C([a,b])$ của các hàm giá trị phức liên tục $f$ và $g$ trên đoạn $[a,b].$ Tích trong của chúng là

\langle f,g\rangle =\int _{a}^{b}f(t){\overline {g(t)}}\,\mathrm {d} t.

Không gian này là không đầy đủ; lấy ví dụ, trên đoạn [−1; 1] với dãy hàm "bước" liên tục ${f k} k$ được xác định bởi:

f_{k}(t)={\begin{cases}0&t\in [-1,0]\\1&t\in \left[{\tfrac {1}{k}},1\right]\\kt&t\in \left(0,{\tfrac {1}{k}}\right)\end{cases}}

Dãy này là một dãy Cauchy với chuẩn tạo bởi tích trong trước không hội tụ thành hàm liên tục.

Biến ngẫu nhiên

Với hai biến ngẫu nhiên $X$ và $Y$ , giá trị kỳ vọng của tích của chúng là một tích trong.^[10]^[11]^[12]

\langle X,Y\rangle =\operatorname {E} (XY)

Trong trường hợp này, $⟨ X, X ⟩ = 0$ khi và chỉ khi $Pr (X = 0) = 1$ (tức là gần như chắc chắn $X = 0$ ). Định nghĩa tích trong dưới dạng giá trị kỳ vọng này còn có thể được mở rộng đối với các vectơ tự do.

Ma trận thực

Với hai ma trận thực vuông cùng cỡ, $⟨ A, B ⟩ ≝ tr(AB T)$ với chuyển vị chính là phép liên hợp, tức là

\left(\langle A,B\rangle =\left\langle B^{\textsf {T}},A^{\textsf {T}}\right\rangle \right)

là một tích trong.

Chuẩn

Không gian tích trong là không gian vectơ định chuẩn với chuẩn (norm) được định nghĩa bởi^[4]

\|x\|={\sqrt {\langle x,x\rangle }}.

Vì với mọi không gian vectơ định chuẩn, không gian tích vô hướng là không gian metric với khoảng cách được định nghĩa bởi

d(x,y)=\|y-x\|.

Các tiên đề của tích trong đảm bảo rằng ánh xạ trên tạo ra một chuẩn, có các tính chất sau.

Tính thuần nhất

Đối với một vectơ

x

thuộc

V

và một vô hướng

r

ta có

\|rx\|=|r|\,\|x\|.

Bất đẳng thức tam giác

Cho các vectơ

x

và

y

thuộc

V

\|x+y\|\leq \|x\|+\|y\|.

Hai tính chất trên cho thấy ta đã có một chuẩn.

Bất đẳng thức Cauchy–Schwarz

Cho

x

,

y

là các phần tử của

V

|\langle x,y\rangle |\leq \|x\|\,\|y\|

với đẳng thức xảy ra khi và chỉ khi

x

và

y

phụ thuộc tuyến tính. Trong các tài liệu toán tiếng Nga, bất đẳng thức này còn được gọi là bất đẳng thức Cauchy–Bunyakovsky hay bất đẳng thức Cauchy–Bunyakovsky–Schwarz.

Công thức phân cực

Tích trong có thể được rút ra từ chuẩn bởi công thức phân cực

\|x+y\|^{2}=\|x\|^{2}+\|y\|^{2}+2\operatorname {Re} \langle x,y\rangle ,

đây là một dạng của định lý cosin.

Trực giao

Hai vectơ là trực giao khi tích trong của chúng bằng 0.
Trong trường hợp không gian vectơ Euclid, là các không gian tích trong hữu hạn chiều trên trường số thực, tích vô hướng cho phép định nghĩa góc (không có chiều) của hai vectơ khác vectơ không bởi

\angle (x,y)=\arccos {\frac {\langle x,y\rangle }{\|x\|\,\|y\|}},

và

0\leq \angle (x,y)\leq \pi .

Định lý Pythagoras

Khi

x

,

y

thuộc

V

và

⟨ x, y ⟩ = 0

, ta có

\|x\|^{2}+\|y\|^{2}=\|x+y\|^{2}.

Chứng minh đẳng thức này yêu cầu chỉ cần biểu diễn định nghĩa chuẩn theo tích trong và thực hiện nhân, sử dụng tính cộng cho từng thành phần. Tên gọi Định lý Pythagoras bắt nguồn từ cách diễn giải trong hình học Euclid.

Đẳng thức Parseval

Sử dụng quy nạp với định lý Pythagoras ta có: nếu

x 1, \dots, x n

là các vectơ trực giao, tức là

⟨ x j, x k ⟩ = 0

với các chỉ số phân biệt

j

,

k

, thì

\sum _{i=1}^{n}\|x_{i}\|^{2}=\left\|\sum _{i=1}^{n}x_{i}\right\|^{2}.

Quy tắc hình bình hành

Cho các phần tử

x

,

y

thuộc

V

, ta có

\|x+y\|^{2}+\|x-y\|^{2}=2\|x\|^{2}+2\|y\|^{2}.

Quy tắc hình bình hành thực chất là một điều kiện cần và đủ cho sự tồn tại một tích trong ứng với một chuẩn cho trước.

Bất đẳng thức Ptolemy

Cho các phần tử

x

,

y

,

z

thuộc

V

, ta có

\|x-y\|\|z\|+\|y-z\|\|x\|\geq \|x-z\|\|y\|.

Bất đẳng thức Ptolemy thực chất cũng là một điều kiện cần và đủ cho sự tồn tại một tích trong tương ứng với một chuẩn cho trước. Cụ thể, Isaac Jacob Schoenberg đã chứng minh vào năm 1952 rằng, cho một không gian thực xác định nửa chuẩn bất kỳ, nếu nửa chuẩn của nó thỏa mãn bất đẳng thức Plotemy thì nửa chuẩn đó chính là chuẩn liên kết với một tích trong.^[13]

Xem thêm

Chú thích

^ By combining the linear in the first argument property with the conjugate symmetry property you get conjugate-linear in the second argument: ${\textstyle \langle x,by\rangle =\langle x,y\rangle {\overline {b}}.}$ This is how the inner product was originally defined and is still used in some old-school math communities. However, all of engineering and computer science, and most of physics and modern mathematics now define the inner product to be linear in the second argument and conjugate-linear in the first argument because this is more compatible with several other conventions in mathematics. Notably, for any inner product, there is some hermitian, positive-definite matrix ${\textstyle M}$ such that ${\textstyle \langle x,y\rangle =x^{*}My.}$ (Here, ${\textstyle x^{*}}$ is the conjugate transpose of ${\textstyle x.}$ )
^ This means that $\langle x,y+z\rangle =\langle x,y\rangle +\langle x,z\rangle$ and $\langle x,ay\rangle ={\overline {a}}\langle x,y\rangle$ for all vectors $x$ , $y$ , and $z$ and all scalars $a$ .
^ A bar over an expression denotes complex conjugation; e.g., ${\textstyle {\overline {x}}}$ is the complex conjugation of ${\textstyle x.}$ For real values, ${\textstyle x={\overline {x}}}$ and conjugate symmetry is just symmetry.
^ Recall that for any complex number $c$ , $c$ is a real number if and only if $c = c$ . Using $y = x$ in condition (2) gives $\langle x,x\rangle ={\overline {\langle x,x\rangle }},$ which implies that $\langle x,x\rangle$ is a real number.
^ This is because condition (1) and positive-definiteness implies that $\langle x,x\rangle$ is always a real number. And as mentioned before, a sesquilinear form is Hermitian if and only if $\langle x,x\rangle$ is real for all $x$ .

Tham khảo

^ ^a ^b ^c ^d ^e ^f ^g ^h ⁱ ^j ^k Trèves 2006, tr. 112-125.
^ Schaefer & Wolff 1999, tr. 40-45.
^ “Compendium of Mathematical Symbols”. Math Vault (bằng tiếng Anh). ngày 1 tháng 3 năm 2020. Truy cập ngày 25 tháng 8 năm 2020.
^ ^a ^b ^c ^d Weisstein, Eric W. “Inner Product”. mathworld.wolfram.com (bằng tiếng Anh). Truy cập ngày 25 tháng 8 năm 2020.
^ Moore, Gregory H. (1995). “The axiomatization of linear algebra: 1875-1940”. Historia Mathematica. 22 (3): 262–303. doi:10.1006/hmat.1995.1025.
^ ^a ^b Schaefer & Wolff 1999, tr. 36-72.
^ Jain, P. K.; Ahmad, Khalil (1995). “5.1 Definitions and basic properties of inner product spaces and Hilbert spaces”. Functional Analysis (ấn bản thứ 2). New Age International. tr. 203. ISBN 81-224-0801-X.
^ Prugovec̆ki, Eduard (1981). “Definition 2.1”. Quantum Mechanics in Hilbert Space (ấn bản thứ 2). Academic Press. tr. 18ff. ISBN 0-12-566060-X.
^ “Inner Product Space | Brilliant Math & Science Wiki”. brilliant.org (bằng tiếng Anh). Truy cập ngày 25 tháng 8 năm 2020.
^ Bigoni, Daniele (2015). “Appendix B: Probability theory and functional spaces” (PDF). Uncertainty Quantification with Applications to Engineering Problems (PhD). Technical University of Denmark. Truy cập ngày 5 tháng 9 năm 2017.
^ Ouwehand, Peter (tháng 11 năm 2010). “Spaces of Random Variables” (PDF). AIMS. Bản gốc (PDF) lưu trữ ngày 5 tháng 9 năm 2017. Truy cập ngày 5 tháng 9 năm 2017.
^ Siegrist, Kyle (1997). “không gian vectơ of Random Variables”. Random: Probability, Mathematical Statistics, Stochastic Processes. Truy cập ngày 5 tháng 9 năm 2017.
^ Apostol, Tom M. (1967). “Ptolemy's Inequality and the Chordal Metric”. Mathematics Magazine (bằng tiếng Anh). 40 (5): 233–235. doi:10.2307/2688275. JSTOR 2688275.

Tham khảo sách

Axler, Sheldon (1997). Linear Algebra Done Right (ấn bản thứ 2). Berlin, New York: Springer-Verlag. ISBN 978-0-387-98258-8.
Emch, Gerard G. (1972). Algebraic Methods in Statistical Mechanics and Quantum Field Theory. Wiley-Interscience. ISBN 978-0-471-23900-0.
Young, Nicholas (1988). An Introduction to Hilbert Space. Cambridge University Press. ISBN 978-0-521-33717-5.

[10] By combining the linear in the first argument property with the conjugate symmetry property you get conjugate-linear in the second argument: ${\textstyle \langle x,by\rangle =\langle x,y\rangle {\overline {b}}.}$ This is how the inner product was originally defined and is still used in some old-school math communities. However, all of engineering and computer science, and most of physics and modern mathematics now define the inner product to be linear in the second argument and conjugate-linear in the first argument because this is more compatible with several other conventions in mathematics. Notably, for any inner product, there is some hermitian, positive-definite matrix ${\textstyle M}$ such that ${\textstyle \langle x,y\rangle =x^{*}My.}$ (Here, ${\textstyle x^{*}}$ is the conjugate transpose of ${\textstyle x.}$ )

[11] This means that $\langle x,y+z\rangle =\langle x,y\rangle +\langle x,z\rangle$ and $\langle x,ay\rangle ={\overline {a}}\langle x,y\rangle$ for all vectors $x$ , $y$ , and $z$ and all scalars $a$ .

[12] A bar over an expression denotes complex conjugation; e.g., ${\textstyle {\overline {x}}}$ is the complex conjugation of ${\textstyle x.}$ For real values, ${\textstyle x={\overline {x}}}$ and conjugate symmetry is just symmetry.

[13] Recall that for any complex number $c$ , $c$ is a real number if and only if $c = c$ . Using $y = x$ in condition (2) gives $\langle x,x\rangle ={\overline {\langle x,x\rangle }},$ which implies that $\langle x,x\rangle$ is a real number.

[14] This is because condition (1) and positive-definiteness implies that $\langle x,x\rangle$ is always a real number. And as mentioned before, a sesquilinear form is Hermitian if and only if $\langle x,x\rangle$ is real for all $x$ .

[FOOTNOTETrèves2006112-125-1] ^ ^a ^b ^c ^d ^e ^f ^g ^h ⁱ ^j ^k Trèves 2006, tr. 112-125.

[FOOTNOTESchaeferWolff199940-45-2] Schaefer & Wolff 1999, tr. 40-45.

[3] “Compendium of Mathematical Symbols”. Math Vault (bằng tiếng Anh). ngày 1 tháng 3 năm 2020. Truy cập ngày 25 tháng 8 năm 2020.

[:0-4] Weisstein, Eric W. “Inner Product”. mathworld.wolfram.com (bằng tiếng Anh). Truy cập ngày 25 tháng 8 năm 2020.

[5] Moore, Gregory H. (1995). “The axiomatization of linear algebra: 1875-1940”. Historia Mathematica. 22 (3): 262–303. doi:10.1006/hmat.1995.1025.

[FOOTNOTESchaeferWolff199936-72-6] Schaefer & Wolff 1999, tr. 36-72.

[Jain-7] Jain, P. K.; Ahmad, Khalil (1995). “5.1 Definitions and basic properties of inner product spaces and Hilbert spaces”. Functional Analysis (ấn bản thứ 2). New Age International. tr. 203. ISBN 81-224-0801-X.

[Prugovec̆ki-8] Prugovec̆ki, Eduard (1981). “Definition 2.1”. Quantum Mechanics in Hilbert Space (ấn bản thứ 2). Academic Press. tr. 18ff. ISBN 0-12-566060-X.

[9] “Inner Product Space | Brilliant Math & Science Wiki”. brilliant.org (bằng tiếng Anh). Truy cập ngày 25 tháng 8 năm 2020.

[15] Bigoni, Daniele (2015). “Appendix B: Probability theory and functional spaces” (PDF). Uncertainty Quantification with Applications to Engineering Problems (PhD). Technical University of Denmark. Truy cập ngày 5 tháng 9 năm 2017.

[16] Ouwehand, Peter (tháng 11 năm 2010). “Spaces of Random Variables” (PDF). AIMS. Bản gốc (PDF) lưu trữ ngày 5 tháng 9 năm 2017. Truy cập ngày 5 tháng 9 năm 2017.

[17] Siegrist, Kyle (1997). “không gian vectơ of Random Variables”. Random: Probability, Mathematical Statistics, Stochastic Processes. Truy cập ngày 5 tháng 9 năm 2017.

[18] Apostol, Tom M. (1967). “Ptolemy's Inequality and the Chordal Metric”. Mathematics Magazine (bằng tiếng Anh). 40 (5): 233–235. doi:10.2307/2688275. JSTOR 2688275.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[note 1]

[note 2]

[note 3]

[note 4]

[note 5]

[10]

[11]

[12]

[13]

x t s Các chủ đề trong Đại số tuyến tính
Khái niệm cơ bản	Vô hướng Vectơ Không gian vectơ Phép nhân vô hướng Chiếu vectơ Hệ sinh Ánh xạ tuyến tính Phép chiếu tuyến tính Độc lập tuyến tính Tổ hợp tuyến tính Cơ sở Chuyển cơ sở Vectơ hàng và cột Không gian hàng và cột Hạt nhân Giá trị riêng và vectơ riêng Ma trận chuyển vị Hệ phương trình tuyến tính
Ma trận	Khối Phân rã Nghịch đảo Định thức con Tích Hạng Biến đổi Quy tắc Cramer Phép khử Gauss
Song tuyến tính	Trực giao Tích vô hướng Không gian tích trong Tích ngoài Quá trình Gram–Schmidt
Đại số đa tuyến tính	Định thức Tích vectơ Tích ba Tích vectơ 7 chiều Đại số hình học Đại số ngoài Song vectơ Đa vectơ Tenxơ Cấu xạ ngoài
Xây dựng không gian vectơ	Không gian đối ngẫu Tổng trực tiếp Không gian hàm Thương Không gian con Tích tenxơ
Đại số tuyến tính số	Floating-point Bình phương tối thiểu tuyến tính Ổn định số Basic Linear Algebra Subprograms Ma trận thưa Comparison of linear algebra libraries
Thể loại Mục lục Chủ đề Toán học Wikibook Wikiversity