
小学生の子どもを持つ保護者にとって、働きながら宿題など勉強のサポートをするのはなかなか大変です。
特に「算数」は、一度苦手意識を持つと後々まで引きずってしまいやすい科目。さらには学年が上がるにつれ一気に内容が難しくなるので、保護者にとっても「どう教えればいいか分からない」となりがちではないでしょうか。
今回は小中高に通う3姉妹を育てながら、長年算数や数学関係の仕事に携わってきたとけいまわりさんに、「小学生への算数の教え方」のヒントを教えていただきました。
こんにちは、とけいまわりといいます。25年以上にわたり教育関係の仕事をしており、主に算数や数学に携わってきました。Xではたびたび、保護者の方からの「子どもに算数や数学を教える際のお悩みや質問」に答えたりもしています。
そこで今回は、小学生の子どもを持つ保護者の方からよく聞くお悩みをもとに「算数の学習をスムーズに進めるためのポイント」を紹介します。宿題の対応や子どもからの質問に悩むみなさんにとって、少しでもヒントになれば幸いです。
小学校低学年で多いのは「基本がなかなか覚えられない」悩み

小学校低学年では「2+3=5など、簡単な足し算がなかなか身に付かない」「九九が覚えられない」といった悩みが多い印象です。
しかしこの頃の子どもはそもそも「まだ小学校での勉強がどういうものなのか分かっていない段階」なので、焦らなくても大丈夫。子どもが理解しやすい方法で、基本をしっかり覚えられるようにサポートしていきましょう。
【お悩み①】足し算が苦手で「指」で計算しようとする

A:指は「数字」を理解するための“いい武器”なので、むしろじゃんじゃん使ってください。ただし「指の形」がよく見えるように、机の上に手を置いて、しっかり指の形を見ながら数えるのが大切です。
大人にも「苦手な足し算」が1つや2つ、あると思います。私はいまだに6+8があやういです。そんなときはむしろ、両手の指をしっかり使って計算していきましょう!
10本の指で足りない場合は周りの方が手伝ってあげてください。
ポイントを詳しく紹介します。
💡コソコソ隠さず、机の上で指の形を見ながら数えよう
数字には「順番」と「量」の2つの役割があります。「い~ち、に~い、さ~ん……」と、「順番」を数えるのは簡単ですが、「2」が1本と1本のまとまり、「3」が1本と1本と1本のまとまり……など「量」の概念を理解するのは、低学年の子どもにとってはまだ難しいんです。
指を見ながら数えるのはこの「量」の概念を理解することにつながります。「ほら、指で数えない! よく考えて!」などといわず、むしろしっかりと机の上に手を乗せて、指の形がよく見えるようにして数え、できたら「よく数えられたね!」と拍手してあげてください。

そのうち、このような指のビジュアルが頭の中に記憶されていきます。

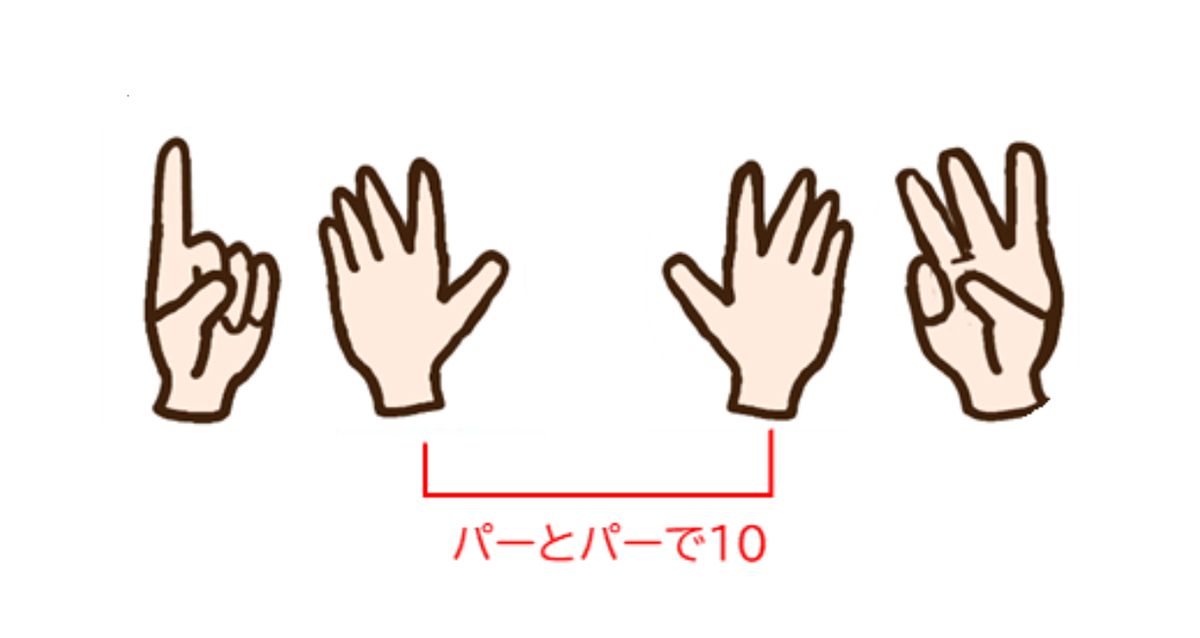
1本1本数えるのが面倒なので、次第に「2と3を合わせると5だな」というように覚えてくるでしょう。特に「パー(5本の指)とパーで10」を覚えておくと、答えが10より大きくなる足し算の際にも便利です。
ちなみに私たちが使っている10進法の起源は、両手の指が10本だからという説もあります。10進法で出される計算に、指を使うのは自然な流れなのかもしれません。
💡「1~5」の足し算を覚えてから「6~9」の足し算へ
「1~5」を使った「答えが10以下」の足し算を繰り返して「2+3は5」などと暗記できるようになってから、「6~9」の数を使った「答えが11以上」の足し算にステップアップします。ここでも同じく机の上に手を置いて、しっかり指のビジュアルを見て覚えましょう。

「7+8」であれば、こんなイメージで「7」と「8」の指の形をそれぞれ作り、数えていきます。先ほどもお話しした「パーとパーで10」が頭の中に入っていれば、あとは残りの数を「1~5」の足し算で計算すればOK。
「パーとパーで10」を覚えていると、いわゆる「さくらんぼ計算(※1)」で10のまとまりを作って計算する際にもスムーズだと思います。
(※1)繰り上がりのある足し算や繰り下がりのある引き算をする際に、1つの数字を2つに分解して計算する方法のこと。計算をする際に使われる図が「さくらんぼの形」に似ていることから「さくらんぼ計算」と呼ばれる。
参考:北海道科学大学「さくらんぼ計算とは?やり方を大学教員が解説!」(詳細)
💡「10よりもっと大きい数の計算」には指ではなく小銭を使う
「40+5」など10よりもっと大きい数になると、周囲の人の手を借りてもなかなか指が足りなくなってきます。そこでおすすめなのが「小銭」を使う方法。

「1円が10枚」で「10円玉1枚」、「10円玉10枚」で「100円玉1枚」になることを押さえておくと、繰り上がりや繰り下がりが小銭を両替するイメージで考えられ、理解しやすくなります。
また「そもそも数字が苦手なのかも?」と感じた場合には、算数に興味を持つきっかけを作ってあげることも効果的だと思います。「位」や「桁」という概念が生まれた歴史を調べると、いろいろ面白い発見が生まれるかと思います
位ができるのには長い歴史があり、0の発明にも時間がかかったといわれています。0がなかった時代には401も41もどちらも「41」と表していたようです。その場の状況で「たぶん41のことを言っているな……」「これは401のことなんだろうな……」と、何となく推測していたんでしょうね。桁の発見って、偉大だったんです。
【お悩み②】九九が覚えられない

子どもが小学2年生になり、九九に苦戦しています……。

A:順番は気にせず、覚えやすい段から覚えましょう。そもそも「九九を覚えること」に疑問を抱いたら、「九九がないと面倒くさい」を、一度経験させてみて。
九九、苦戦しますよね。算数の最初の難関!
足し算と同じく、私もいまだに7×6があやういです。しじゅう……の後は、一か八かで答えを言ってます。
ちなみに私が一番好きな九九は、3×7=21です! 素朴さの中にも鋭さがあり、とてもシャープでエッジがきいている感じがします!
💡「覚えやすい段」から覚えよう
九九を覚える際のポイントは、必ずしも1の段から覚えなくてもいいこと。私のおすすめは5の段。1の位が「5」か「0」かなので、とても覚えやすいんです。
覚え方ですが、わが家では「にいちがに♪ ににんがし〜♪ にさんがろく〜♪」のように歌に乗せて覚えていました。
💡「同じ数を何度も足すのがかけ算」を「面倒くささ」で理解する
お子さんが「なんで九九なんて覚えなきゃいけないの?」と疑問を抱くこともあるかと思います。
そんなときは「5を9回足してみて」など、九九を使わずに「同じ数を何度も足す」ことを経験させて、面倒くささを理解してもらうといいでしょう。

「5+5+5+5+5+5+5+5+5……」面倒くさいですよね。このような問題を何問か解いてみてから「九九を使えば、5を9回足すのを『5×9=45』って一発で答えられるんだよ!」という流れで教えるのがいいかと思います。
そもそも、算数と数学の歴史は「これ、面倒くさいね」からの「じゃあ、新しい計算方法を生み出しといたよ!」の繰り返し。九九はもちろん、後に出てくるサイン・コサインや、log、ベクトル、その他さまざまな公式や解き方も「こりゃあ便利だ!」が原点です。
「数学なんて日常生活で使わないじゃん!」と思う方も多いかもしれませんが、「サイン・コサイン なぜ必要」とか「サイン・コサイン どこで使う」などで検索すると「なるほど、これがないと家が建てられなくなるんだな……」などなど、いろいろな気付きがあると思います。
とはいえ「なるほど、九九の大切さが分かったよ!」みたいな素直な展開にはなかなかならないでしょうが、面倒なことを簡単に処理できるようにするのが算数や数学なんだと、何となく実感してもらえたらなと思います。
小学校中学年〜高学年になり「ついていけない」と感じたら

小学校中学年以上になってくるとどんどん内容が高度になり「親も教えるのが難しい」という場面が出てきます。そんなときは「算数との向き合い方」を少し変えてみるのがいいでしょう。
【お悩み③】学習の難易度が急に上がってしまった

Q:分数など、急に学習内容が難しくなり、勉強についていけなくなってしまいました……。

A:小学校中〜高学年になると、どんどん抽象的な単元に入っていきます。数学は、最終的に「抽象的なものを理解する力を育てているのだ」という理解をしつつ「困ったら戻る」習慣をつけましょう。
人生で最初に出会う「抽象的概念」が「0」、その次は「分数」だと思います。
分数は「3つに分けた内の1つ」というような概念。今まで出会ったことのない「1個、2個が通用しない世界」を小学生から理解するのはスーパーハードです。Xでも分数に対する憎しみ、もとい質問や疑問はよく寄せられます。保護者のみなさんも、かつて苦戦した経験があるのでしょう。
分数は、足し算・かけ算・割り算でそれぞれやり方が違って、いちいち面倒くさい。そして、何をやっているのか見えにくい。ここで「まあ、そういうもんがあるんだろうな」と思うか「何それ!イメージできない! もう無理!」になるかで道が分かれがちです。
💡1個、2個と数えられない「抽象的概念」を子どもにどう理解させるか
算数や数学は「よく分からないものを理解する論理的思考」が身に付く科目であり、その第一歩が分数です。
ここから算数や数学は「1個、2個と数えられる単元」から「1個、2個と数えられない『抽象的な単元』」へと段階的に進み、最終的にはルートや虚数など「この世には存在しないけれども、それが“ある”とすれば世界が大きく開くため、人類が作った数学的な概念」へと進みます。

「リンゴなら分かる」から、「リンゴでなくても理解できた」のワンステップが大事です。
💡困ったときには一度戻って「単純な数字」で仕組みを理解する
では、このような抽象的概念に向き合っていくにはどうするか。困ったときは、1個2個と数えられる世界に戻ればOKです。
例えば「6÷1/2」が何を計算しているのか困ったら、6÷2に戻ってみましょう。「6÷2は、6個のリンゴを2個ずつ分けると、3人分になる」ので、6÷2=3です。
6÷1/2も同じように考えます。「6個のリンゴを1/2個(半分)ずつ分けると、12人分になる」ので、6÷1/2=12です。

このように、分数が苦手な場合はまず、「半分」でイメージしやすい「1/2」から考え始めるといいでしょう。まずは単純な数字を使って、仕組みを理解してもらうのです。
1/2よりも複雑な分数になると頭の中でイメージが難しくなり、リンゴで説明しようとすると余計に分かりにくくなってしまうことがあります。その場合には、ジュース・牛乳などの液体や小麦粉などの粉、もしくはカットしやすいピザなど、問題によってイメージしやすいもので説明するとよいでしょう。
💡速度など「単位量あたりの大きさ」も、まずは「単純な数字」で考える
個人的に分数よりもやっかいなのが「1人あたり」「1時間あたり」などの量を求める「単位量あたりの大きさ」。これに一度つまずくと後々ずっとひきずることになるので、ゆっくりと時間を取って勉強しておきたいところです。
「60km/時(時速60km)」という速さを例に挙げてみます。
「速さ」は目に見えません。そこで「速さ」が目に見えるように「1時間でどのくらいの距離を進んだか」という「進んだ距離」でスピードを表したものが「km/時」です。公式だと「距離=速さ×時間」で計算できますが、いきなり公式を覚えさせてもとっつきづらいだけです。
1時間で60km進めるのだから、2時間では120km、30分だったら1時間の半分の30km、15分ではさらに半分の15km……のように、公式を使う前にまず「1つで〇〇だから、2つでは、半分では……」と考えていくのがいいでしょう。そのときは、できるだけ「分かりやすい単純な数字」で考えるのがおすすめです。
また、土日の余裕のあるタイミングなどに一緒にごはんを作りながら「1人前だとお肉が80g。うちは4人家族だから何g必要かな?」など、実践的に「単位量あたりの大きさ」を学ぶ機会を作るのもいいと思います。
「つまずいたら基本に戻る」が実は近道に

算数と数学は、良くも悪くも段階的に登っていく、らせん階段形式の学問です。さらには関数、図形、確率などいろいろなジャンルごとに何本もらせん階段があり、そのらせん階段同士もあちこちでつながっています。
そのためゆっくり登れば登りやすいのですが、一度見失って授業が先に進んでしまうと、後からなかなか追いつけなくなります。
少しでも「階段を上がりづらくなった」と感じたら焦らずに、何階か下ってください。それが一番の近道だと思います。
中学生になり数学の二次関数につまずいたら、同じ「関数とグラフ」のジャンルで一次関数、比例のグラフへ少しずつ下がり、小学校の教科書まで戻ってみましょう。意外と大切なことが抜けていたりします(ということで、小学校の教科書はすぐに処分しない方がいいです)。
また、テレビやYouTubeなど視覚的に学べる教育系の番組はとても参考になります。参考書に書いてあることが分からなくても、動画を見ればスッと理解できることも多いでしょう。
他にも最近は、分かりやすい解説サイトがたくさんあります。「三角比とは いつ使う」「ベクトルとは 簡単に」「対数の生まれたわけ」など、概念や成り立ちについての素朴な疑問をインターネットで検索するのも、理解の助けになると思います。
全てに納得しないと前に進めないお子さん、よく分からないのに式を立ててしまうお子さんなど、いろいろなお子さんがいらっしゃるかと思います。
全てに納得したいタイプのお子さんには「じっくりゆっくり焦らずに」、分からないのに式を立ててしまうお子さんには「簡単な分かりやすい数字で1回確認をしてから問題に当たる」など、お子さんごとに適した対策があります。いろいろ親子で試しながら、ベターなやり方をつかんでいってください。うちもいまだに手探り状態ですが(笑)。
家庭でサポートするより、いっそ塾に通わせる方が学びやすい子もいるかと思います。気負わず、お子さんに合ったベストスタイルを探って算数・数学ライフを楽しんでみてください。
記事トップ&解説イラスト:とけいまわり
編集:はてな編集部
働きながら、小学生の子どもをサポートするヒント
りっすん by イーアイデム
Xも更新中!
Follow @shinkokyulisten
<Facebookページも更新中> @shinkokyulisten






Q:足し算が苦手でいつまでたっても「指」を使います。いくら言ってもこっそり使うのですが、どうしたらいいでしょう?