121 (number)

← 120 121 122 →
← 120 121 122 123 124 125 126 127 128 129 → List of numbers — Integers ← 0 100 200 300 400 500 600 700 800 900 →
Cardinal	one hundred twenty-one
Ordinal	121st (one hundred and twenty-first)
Factorization	112
Divisors	1, 11, 121
Roman numeral	CXXI
Binary	11110012
Ternary	111113
Quaternary	13214
Quinary	4415
Senary	3216
Octal	1718
Duodecimal	A112
Hexadecimal	7916
Vigesimal	6120
Base 36	3D36

121 (one hundred [and] twenty-one) is the natural number following 120 and preceding 122.

In mathematics

One hundred [and] twenty-one is a square and is the sum of three consecutive primes (37 + 41 + 43). There are no squares besides 121 known to be of the form 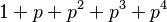$1 + p + p^2 + p^3 + p^4$, where p is prime (3, in this case). Other such squares must have at least 35 digits.

There are only two other squares known to be of the form n! + 1, supporting Brocard's conjecture. Another example of 121 being of the few examples supporting a conjecture is that Fermat conjectured that 4 and 121 are the only perfect squares of the form x³ - 4 (with x being 2 and 5, respectively).

It is also a star number and a centered octagonal number.

A Chinese checkers board has 121 holes

In base 10, it is a Smith number since its digits add up to the same value as its factorization (which uses the same digits) and as a consequence of that it is a Friedman number (11^2). But it can not be expressed as the sum of any other number plus that number's digits, making 121 a self number.

In other fields

121 is also:

• The electricity emergency telephone number in Egypt
• The number for voicemail for mobile phones on the Vodafone network
• The undiscovered chemical element Unbiunium has the atomic number 121
• The official end score for Cribbage

See also

• List of highways numbered 121
• United States House of Representatives House Resolution 121
• United Nations Security Council Resolution 121