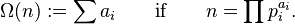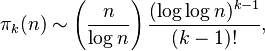Almost prime

In number theory, a natural number is called almost prime if there exists an absolute constant K such that the number has at most K prime factors. An almost prime n is denoted by P_r if and only if the number of prime factors of n, counted according to multiplicity, is at most r. A natural number is called k-almost prime if it has exactly k prime factors, counted with multiplicity. More formally, a number n is k-almost prime if and only if Ω(n) = k, where Ω(n) is the total number of primes in the prime factorization of n:

$\Omega(n) := \sum a_i \qquad\mbox{if}\qquad n = \prod p_i^{a_i}.$

A natural number is thus prime if and only if it is 1-almost prime, and semiprime if and only if it is 2-almost prime. The set of k-almost primes is usually denoted by P_k. The smallest k-almost prime is 2^k. The first few k-almost primes are:

k	k-almost primes	OEIS sequence
1	2, 3, 5, 7, 11, 13, 17, 19, …	A000040
2	4, 6, 9, 10, 14, 15, 21, 22, …	A001358
3	8, 12, 18, 20, 27, 28, 30, …	A014612
4	16, 24, 36, 40, 54, 56, 60, …	A014613
5	32, 48, 72, 80, 108, 112, …	A014614
6	64, 96, 144, 160, 216, 224, …	A046306
7	128, 192, 288, 320, 432, 448, …	A046308
8	256, 384, 576, 640, 864, 896, …	A046310
9	512, 768, 1152, 1280, 1728, …	A046312
10	1024, 1536, 2304, 2560, …	A046314
11	2048, 3072, 4608, 5120, …	A069272
12	4096, 6144, 9216, 10240, …	A069273
13	8192, 12288, 18432, 20480, …	A069274
14	16384, 24576, 36864, 40960, …	A069275
15	32768, 49152, 73728, 81920, …	A069276
16	65536, 98304, 147456, …	A069277
17	131072, 196608, 294912, …	A069278
18	262144, 393216, 589824, …	A069279
19	524288, 786432, 1179648, …	A069280
20	1048576, 1572864, 2359296, …	A069281

The number π_k(n) of positive integers less than or equal to n with at most k prime divisors (not necessarily distinct) is asymptotic to:

$\pi_k(n) \sim \left( \frac{n}{\log n} \right) \frac{(\log\log n)^{k-1}}{(k - 1)!},$

a result of Landau. See also the Hardy–Ramanujan theorem.

External links

• Weisstein, Eric W., "Almost prime", MathWorld.