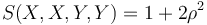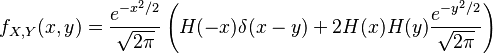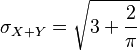Cokurtosis

In probability theory and statistics, cokurtosis is a measure of how much two random variables change together. Cokurtosis is the fourth standardized cross central moment. If two random variables exhibit a high level of cokurtosis they will tend to undergo extreme positive and negative deviations at the same time.

Definition

For two random variables X and Y there are three non-trivial cokurtosis statistics

$K(X,X,X,Y) = {\operatorname{E}{\big[(X - \operatorname{E}[X])^3(Y - \operatorname{E}[Y])\big]} \over \sigma_X^3 \sigma_Y},$

$K(X,X,Y,Y) = {\operatorname{E}{\big[(X - \operatorname{E}[X])^2(Y - \operatorname{E}[Y])^2\big]} \over \sigma_X^2 \sigma_Y^2},$

and

$K(X,Y,Y,Y) = {\operatorname{E}{\big[(X - \operatorname{E}[X])(Y - \operatorname{E}[Y])^3\big]} \over \sigma_X \sigma_Y^3},$

where E[X] is the expected value of X, also known as the mean of X, and $\sigma_X$ is the standard deviation of X.

Properties

• Kurtosis is a special case of the cokurtosis when the two random variables are identical:

$K(X,X,X,X) = {\operatorname{E}{\big[(X - \operatorname{E}[X])^4\big]} \over \sigma_X^4} = {\operatorname{kurtosis}\big[X\big]},$

• For two random variables, X and Y, the kurtosis of the sum, X + Y, is

Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \begin{align} K_{X+Y} = {1 \over \sigma_{X+Y}^4} \big[ & \sigma_X^4K_X + 4\sigma_X^3\sigma_YK(X,X,X,Y) + 6\sigma_X^2\sigma_Y^2K(X,X,Y,Y) \\ & {} + 4\sigma_X\sigma_Y^3K(X,Y,Y,Y) + \sigma_Y^4K_Y \big], \end{align}

where 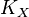$K_X$ is the kurtosis of X and $\sigma_X$ is the standard deviation of X.

• It follows that the sum of two random variables can have kurtosis different from 3 ($K_{X+Y} \neq 3$) even if both random variables are have kurtosis of 3 in isolation ($K_X = 3$ and $K_Y = 3$).
• The cokurtosis between variables X and Y does not depend on the scale on which the variables are expressed. If we are analyzing the relationship between X and Y, the cokurtosis between X and Y will be the same as the cokurtosis between a + bX and c + dY, where a, b, c and d are constants.

Examples

Bivariate normal distribution

Let X and Y each be normally distributed with correlation coefficient ρ. The cokurtosis terms are

$S(X,X,Y,Y) = 1+2\rho^2$

$S(X,X,X,Y) = S(X,Y,Y,Y) = 3\rho$

Since the cokurtosis depends only on ρ, which is already completely determined by the lower-degree covariance matrix, the cokurtosis of the bivariate normal distribution contains no new information about the distribution. It is a convenient reference, however, for comparing to other distributions.

Nonlinearly correlated normal distributions

Let X be standard normally distributed and Y be the distribution obtained by setting X=Y whenever X<0 and drawing Y independently from a standard half-normal distribution whenever X>0. In other words, X and Y are both standard normally distributed with the property that they are completely correlated for negative values and uncorrelated apart from sign for positive values. The joint probability density function is

$f_{X,Y}(x,y) = \frac{e^{-x^2/2}}{\sqrt{2\pi}} \left(H(-x)\delta(x-y) + 2H(x)H(y) \frac{e^{-y^2/2}}{\sqrt{2\pi}}\right)$

where H(x) is the Heaviside step function and δ(x) is the Dirac delta function. The fourth moments are easily calculated by integrating with respect to this density:

$S(X,X,Y,Y) = 2$

$S(X,X,X,Y) = S(X,Y,Y,Y) = \frac{3}{2}+\frac{2}{\pi} \approx 2.137$

It is useful to compare this result to what would have been obtained for an ordinary bivariate normal distribution with the usual linear correlation. From integration with respect to density, we find that the linear correlation coefficient of X and Y is

$\rho = \frac{1}{2} + \frac{1}{\pi} \approx 0.818$

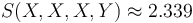A bivariate normal distribution with this value of ρ would have $S(X,X,Y,Y) \approx 2.455$ and $S(X,X,X,Y) \approx 2.339$. Therefore all of the cokurtosis terms of this distribution with this nonlinear correlation are smaller than what would have been expected from a bivariate normal distribution with ρ=0.818.

Note that although X and Y are individually standard normally distributed, the distribution of the sum X+Y is platykurtic. The standard deviation of the sum is

$\sigma_{X+Y} = \sqrt{3 + \frac{2}{\pi}}$

Inserting that and the individual cokurtosis values into the kurtosis sum formula above, we have

$K_{X+Y} = \frac{2\pi(8+15\pi)}{(2+3\pi)^2} \approx 2.654$

This can also be computed directly from the probability density function of the sum:

$f_{X+Y}(u) = \frac{e^{-u^2/8}}{2\sqrt{2\pi}} H(-u) + \frac{e^{-u^2/4}}{\sqrt{\pi}} \operatorname{erf}\left(\frac{u}{2}\right) H(u)$

See also

• Moment (mathematics)
• Coskewness

Further reading

Volume 8, Issue 1, March 2001, Pages 55–81