Conway polyhedron notation

This example chart shows how 11 new forms can be derived from the cube using 3 operations. The new polyhedra are shown as maps on the surface of the cube so the topological changes are more apparent. Vertices are marked in all forms with circles.

This chart adds 3 more operations: George Hart's p=propellor operator that add quadrilaterals, g=gyro operation that creates pentagons, and a c=Chamfer operation that replaces edges with hexagons

Conway polyhedron notation is used to describe polyhedra based on a seed polyhedron modified by various operations.

The seed polyhedra are the Platonic solids, represented by the first letter of their name (T,O,C,I,D); the prisms (Pn), antiprisms (An) and pyramids (Yn). Any convex polyhedron can serve as a seed, as long as the operations can be executed on it.

John Conway extended the idea of using operators, like truncation defined by Kepler, to build related polyhedra of the same symmetry. His descriptive operators can generate all the Archimedean solids and Catalan solids from regular seeds. Applied in a series, these operators allow many higher order polyhedra to be generated.

Operations on polyhedra

Elements are given from the seed (v,e,f) to the new forms, assuming seed is a convex polyhedron: (a topological sphere, Euler characteristic = 2) An example image is given for each operation, based on a cubic seed. The basic operations are sufficient to generate the reflective uniform polyhedra and theirs duals. Some basic operations can be made as composites of others.

Special forms

The kis operator has a variation, kn, which only adds pyramids to n-sided faces.

The truncate operator has a variation, tn, which only truncates order-n vertices.

The operators are applied like functions from right to left. For example a cuboctahedron is an ambo cube, i.e. t(C) = aC, and a truncated cuboctahedron is t(a(C)) = t(aC) = taC.

Basic operations

Operator	Example		Name	Alternate construction	vertices	edges	faces	Description
			Seed		v	e	f	Seed form
d		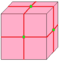	dual		f	e	v	dual of the seed polyhedron - each vertex creates a new face
a		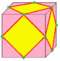	ambo		e	2e	2 + e	New vertices are added mid-edges, while old vertices are removed. (rectify)
j			join	da	e + 2	2e	e	The seed is augmented with pyramids at a height high enough so that 2 coplanar triangles from 2 different pyramids share an edge.
t		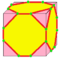	truncate	dkd	2e	3e	e + 2	truncate all vertices. conjugate kis
k		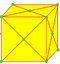	kis	dtd	e + 2	3e	2e	raises a pyramid on each face.
i		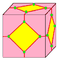	--	dk	2e	3e	e + 2	Dual of kis. (bitruncation)
n		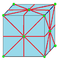	--	kd	e + 2	3e	2e	Kis of dual
e		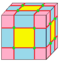	expand	aa = aj	2e	4e	2e + 2	Each vertex creates a new face and each edge creates a new quadrilateral. (cantellate)
o			ortho	de = ja = jj	2e + 2	4e	2e	Each n-gon faces are divided into n quadrilaterals.
b			bevel	ta	4e	6e	2e + 2	New faces are added in place of edges and vertices. (cantitruncation)
m			meta	db = kj	2e + 2	6e	4e	n-gon faces are divided into 2n triangles

Extended operators

These extended operators can't be created in general from the basic operations above. Some can be created in special cases with k and t operators only applied to specific sided faces and vertices. For example a chamfered cube, cC, can be constructed as t4daC, as a rhombic dodecahedron, daC or jC, with its valence-4 vertices truncated. And a quinto-dodecahedron, qD can be constructed as t5daaD or t5deD or t5oD, a deltoidal hexecontahedron, deD or oD, with its valence-5 vertices truncated.

Extended operations

Operator	Example		Name	Alternate construction	vertices	edges	faces	Description
			Seed		v	e	f	Seed form
c			chamfer		v + 2e	4e	f + e	An edge-truncation. New hexagonal faces are added in place of edges.
-		Error creating thumbnail: File missing	-	dc	f + e	4e	v + 2e	Dual of chamfer
q		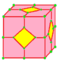	quinto		v+3e	6e	f+2e	Ortho followed by truncation of vertices centered on original faces. This create 2 new pentagons for every original edge.
-			-	dq	f+2e	6e	v+3e	Dual of quinto

Chiral extended operators

These extended operators can't be created in general from the basic operations above. The gyro/snub operations are needed to generate the uniform polyhedra and duals with rotational symmetry.

Geometric artist George W. Hart created an operation he called a propellor, and another reflect to create mirror images of the rotated forms.

• p – "propellor" (A rotation operator that creates quadrilaterals at the vertices). This operation is self-dual: dpX=pdX.
• r – "reflect" – makes the mirror image of the seed; it has no effect unless the seed was made with s or g.

The half operator, h, from Coxeter, reduces square faces into digons, with two coinciding edges, which may or may not be replaced by a single edge. If digons remain, subsequently truncation operations can expand digons into square faces.

Chiral extended operations

Operator	Example		Name	Alternate construction	vertices	edges	faces	Description
			Seed		v	e	f	Seed form
r			reflect (Hart)		v	e	f	Mirror image for chiral forms
h		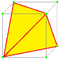	half *		v/2	e	f+v/2	Alternation, remove half vertices, limited to seed polyhedra with even-sided faces
p		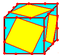	propellor (Hart)		v + 2e	4e	f + e	A face rotation that creates quadrilaterals at vertices (self-dual)
-			-	dp = pd	f + e	4e	v + 2e
s			snub	dg = hta	2e	5e	3e + 2	"expand and twist" – each vertex creates a new face and each edge creates two new triangles
g		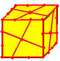	gyro	ds	3e + 2	5e	2e	Each n-gon face is divided into n pentagons.
w		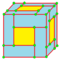	whirl		v+4e	7e	f+2e	Gyro followed by truncation of vertices centered on original faces. This create 2 new hexagons for every original edge
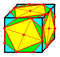-			-	dw	f+2e	7e	v+4e	Dual of whirl

Generating regular seeds

All of the five regular polyhedra can be generated from prismatic generators with zero to two operators:

• Triangular pyramid: Y3 (A tetrahedron is a special pyramid)
  • T = Y3
  • O = aY3 (ambo tetrahedron)
  • C = jY3 (join tetrahedron)
  • I = sY3 (snub tetrahedron)
  • D = gY3 (gyro tetrahedron)
• Triangular antiprism: A3 (An octahedron is a special antiprism)
  • O = A3
  • C = dA3
• Square prism: P4 (A cube is a special prism)
  • C = P4
• Pentagonal antiprism: A5
  • I = k5A5 (A special gyroelongated dipyramid)
  • D = t5dA5 (A special truncated trapezohedron)

The regular Euclidean tilings can also be used as seeds:

• Q = Quadrille =Square tiling
• H = Hextille = Hexagonal tiling = dΔ
• Δ = Deltille = Triangular tiling = dH

Examples

The cube can generate all the convex uniform polyhedra with octahedral symmetry. The first row generates the Archimedean solids and the second row the Catalan solids, the second row forms being duals of the first. Comparing each new polyhedron with the cube, each operation can be visually understood. (Two polyhedron forms don't have single operator names given by Conway.)

Cube "seed"	ambo	truncate	bitruncate	expand	bevel
C	aC = djC	tC = dkdC	tdC = dkC	eC = aaC = doC	bC = taC = dmC = dkjC
dual	join	dual truncate	kis	ortho	meta
dC	jC	kdC = dtC	kC	oC	mC
Extended operations
snub	propellor	chamfer	whirl
sC	pC	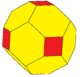cC	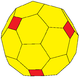wC
gyro	dual propeller	dual chamfer	dual whirl
gC = dsC	dpC	dcC	dwC

Tetrahedron seed (T)

T	tT	aT	tdT	eT	bT	sT
dT	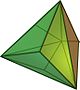dtT	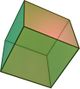jT	kT	oT	mT	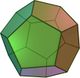gT

The truncated icosahedron as a nonregular seed creates more polyhedra which are not vertex or face uniform.

Truncated icosahedron seed

"seed"	ambo	truncate	bitruncate	expand	bevel
tI	80px atI	ttI	tdtI	etI	80px btI
dual	join		kis	ortho	meta
dtI	jtI	kdtI	ktI	otI	mtI
Extended operations
snub	propellor	chamfer	quinto	whirl
80px stI	ptI	ctI	qtI	wtI
gyro	dual propeller	dual chamfer	dual quinto	dual whirl
gtI	dptI	dctI	dqtI	dwtI

Geometric coordinates of derived forms

In general the seed polyhedron can be considered a tiling of a surface since the operators represent topological operations so the exact geometric positions of the vertices of the derived forms are not defined in general. A convex regular polyhedron seed can be considered a tiling on a sphere, and so the derived polyhedron can equally be assumed to be positioned on the surface of a sphere. Similar a regular tiling on a plane, such as a hexagonal tiling can be a seed tiling for derived tilings. Nonconvex polyhedra can become seeds if a related topological surface is defined to constrain the positions of the vertices. For example toroidal polyhedra can derive other polyhedra with point on the same torus surface.

Spherical examples

Example: A dodecahedron seed as a spherical tiling

D	tD	aD	tdD	eD	taD	sD
dD	dtD	daD = jD	dtdD = kD	deD = oD	dtaD = mD	gD

Euclidean examples

Example: A Euclidean hexagonal tiling seed (H)

H	tH	aH	tdH = H	eH	taH = bH	sH
dH	dtH	daH = jH	dtdH = kH	deH = oH	dtaH = mH	dsH = gH

Hyperbolic examples

Example: A hyperbolic heptagonal tiling seed

{7,3} "seed"	truncate	ambo	bitruncate	expand	bevel	snub
dual	dual kis	join	kis	ortho	meta	gyro

Other polyhedra

Iterating operators on simple forms can produce progressively larger polyhedra, maintaining the fundamental symmetry of the seed element. The vertices are assumed to be on the same spherical radius. Some generated forms can exist as spherical tilings, but fail to produce polyhedra with planar faces.

Tetrahedral symmetry

• 

  t6dtT

• 

  atT

• 

  tatT

• 

  stT

Octahedral symmetry

• 

  t4daC

• 

  k4aC

• 

  dk4sC

• 

  t3daC

• 

  taaC

• 

  saC

• 

  atO

• Truncated rectified truncated octahedron.png

  tatO

• Snub rectified truncated octahedron.png

  stO

• Rectified truncated cube.png

  atC

• Truncated rectified truncated cube.png

  tatC

• Snub rectified truncated cube.png

  stC

• 

  daC

• 

  edaC

• 

  gaC

• 

  saC

Icosahedral symmetry

• Truncated rhombicosidodecahedron.png

  taaD

• Snub rhombicosidodecahedron.png

  saD

• Rectified truncated icosahedron.png

  atI

• Truncated rectified truncated icosahedron.png

  tatI

• Snub rectified truncated icosahedron.png

  stI

• Rectified truncated dodecahedron.png

  atD

• Truncated rectified truncated dodecahedron.png

  tatD

• Snub rectified truncated dodecahedron.png

  stD

• 

  daD

• 

  edaD

• 

  gaD

• 

  saD

• Rectified truncated kissed dodecahedron.png

  atkD

• Rectified chamfered truncated icosahedron.png

  actI

Rhombic:

• Rhombic enneacontahedron.png

  Rhombic enneacontahedron
  dakD

• 

  t3daD

Triangular:

• 

  kD

• Pentakis icosidodecahedron.png

  k5aD

• 

  k6k5tI

• 

  kt5daD

• 

  kdktI

• 

  kdkt5daD

Dual triangular:

• 

  dkD

• 

  t5daD=cD

• 

  dk6k5tI

• 

  dkt5daD

• 

  tktI

• 

  tkt5daD

Triangular chiral:

• 

  dsD

• 

  k5sD

• 

  k5k6stI=kdk5sD

Dual triangular chiral:

• 

  sD

• 

  dk5sD

• 

  dk5k6stI=tk5sD

Dihedral symmetry

• 

  t4daA4=cA4

• 

  t4daA4=cA4 (side)

• 

  t4daA4=cA4 (top)

• 

  tA4

• 

  tA5

• 

  ssA2

• 

  ssA3=I

• 

  ssA4

• 

  ssA5

• 

  aaP3

• 

  aaA4

See also

• Uniform polyhedra
• Computer graphics algorithms:
  • Doo–Sabin subdivision surface – expand operator
  • Catmull–Clark subdivision surface – ortho operator
• Goldberg polyhedron

References

• George W. Hart, Sculpture based on Propellorized Polyhedra, Proceedings of MOSAIC 2000, Seattle, WA, August, 2000, pp. 61–70 [1]
• John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, The Symmetries of Things 2008, ISBN 978-1-56881-220-5
  • Chapter 21: Naming the Archimedean and Catalan polyhedra and Tilings

External links and references

• George Hart's Conway interpreter: generates polyhedra in VRML, taking Conway notation as input. Also includes helpful explanations of the operations.
  • Polyhedra Names
• Vertex- and edge-truncation of the Platonic and Archimedean solids leading to vertex-transitive polyhedra Livio Zefiro
• polyHédronisme: generates polyhedra in HTML5 canvas, taking Conway notation as input
• Weisstein, Eric W., "Conway Polyhedron Notation", MathWorld.
• John Conway's notation
• Weisstein, Eric W., "Truncation", MathWorld. (truncate)
• Weisstein, Eric W., "Rectification", MathWorld. (ambo)
• Weisstein, Eric W., "Cumulation or Apiculation", MathWorld. (kis)
• Conway operators, PolyGloss, Wendy Krieger
• Derived Solids