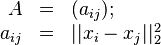Euclidean distance matrix

In mathematics, a Euclidean distance matrix is an n×n matrix representing the spacing of a set of n points in Euclidean space. If A is a Euclidean distance matrix and the points 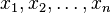$x_1,x_2,\ldots,x_n$ are defined on m-dimensional space, then the elements of A are given by

$\begin{array}{rll} A & = & (a_{ij}); \\ a_{ij} & = & ||x_i - x_j||_2^2 \end{array}$

where ||.||₂ denotes the 2-norm on R^m.

Properties

Simply put, the element $a_{ij}$ describes the square of the distance between the i ^th and j ^th points in the set. By the properties of the 2-norm (or indeed, Euclidean distance in general), the matrix A has the following properties.

• All elements on the diagonal of A are zero (i.e. it is a hollow matrix).
• The trace of A is zero (by the above property).
• A is symmetric (i.e. $a_{ij} = a_{ji}$).
• $\sqrt{a_{ij}} \le \sqrt{a_{ik}} + \sqrt{a_{kj}}$ (by the triangle inequality)
• $a_{ij}\ge 0$
• The number of unique (distinct) non-zero values within an n-by-n Euclidean distance matrix is bounded above by $n(n-1)/2$ due to the matrix being symmetric and hollow.
• In dimension m, a Euclidean distance matrix has rank less than or equal to m+2. If the points 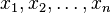$x_1,x_2,\ldots,x_n$ are in general position, the rank is exactly min(n, m + 2).

See also

• Adjacency matrix
• Coplanarity
• Distance geometry
• Distance matrix
• Euclidean random matrix
• Classical multidimensional scaling, a visualization technique that approximates an arbitrary dissimilarity matrix by a Euclidean distance matrix