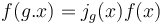Factor of automorphy
In mathematics, the notion of factor of automorphy arises for a group acting on a complex-analytic manifold. Suppose a group  acts on a complex-analytic manifold
acts on a complex-analytic manifold 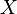 . Then,
. Then,  also acts on the space of holomorphic functions from
also acts on the space of holomorphic functions from 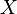 to the complex numbers. A function
to the complex numbers. A function 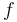 is termed an automorphic form if the following holds:
is termed an automorphic form if the following holds:
where 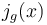 is an everywhere nonzero holomorphic function. Equivalently, an automorphic form is a function whose divisor is invariant under the action of
is an everywhere nonzero holomorphic function. Equivalently, an automorphic form is a function whose divisor is invariant under the action of  .
.
The factor of automorphy for the automorphic form 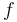 is the function
is the function 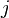 . An automorphic function is an automorphic form for which
. An automorphic function is an automorphic form for which 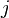 is the identity.
is the identity.
Some facts about factors of automorphy:
- Every factor of automorphy is a cocycle for the action of
 on the multiplicative group of everywhere nonzero holomorphic functions.
on the multiplicative group of everywhere nonzero holomorphic functions. - The factor of automorphy is a coboundary if and only if it arises from an everywhere nonzero automorphic form.
- For a given factor of automorphy, the space of automorphic forms is a vector space.
- The pointwise product of two automorphic forms is an automorphic form corresponding to the product of the corresponding factors of automorphy.
Relation between factors of automorphy and other notions:
- Let
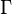 be a lattice in a Lie group
be a lattice in a Lie group  . Then, a factor of automorphy for
. Then, a factor of automorphy for 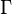 corresponds to a line bundle on the quotient group
corresponds to a line bundle on the quotient group  . Further, the automorphic forms for a given factor of automorphy correspond to sections of the corresponding line bundle.
. Further, the automorphic forms for a given factor of automorphy correspond to sections of the corresponding line bundle.
The specific case of 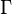 a subgroup of SL(2, R), acting on the upper half-plane, is treated in the article on automorphic factors.
a subgroup of SL(2, R), acting on the upper half-plane, is treated in the article on automorphic factors.
References
- Lua error in package.lua at line 80: module 'strict' not found. (The commentary at the end defines automorphic factors in modern geometrical language)
- Lua error in package.lua at line 80: module 'strict' not found.