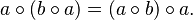Flexible algebra

In mathematics, a flexible binary operation 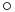$\circ$ is a binary operation that satisfies the equation

$a \circ \left( b \circ a \right) = \left( a \circ b \right) \circ a .$

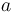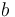for any two elements $a$ and $b$ of an algebraic structure.

Every commutative or associative operation is flexible, so the flexible identity becomes important for binary operations that are neither commutative nor associative, e.g. for the multiplication of sedenions, which are not even alternative.

Examples

The following classes of algebra are flexible:

• Alternative algebra
• Lie algebras
• Jordan algebras
• Okubo algebras

See also

• Zorn ring
• Maltsev algebra