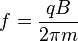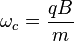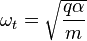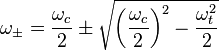Fourier transform ion cyclotron resonance
| Acronym | FTICR |
|---|---|
| Classification | Mass spectrometry |
| Other techniques | |
| Related | Ion trap Quadrupole ion trap Penning trap Orbitrap |
Fourier transform ion cyclotron resonance mass spectrometry is a type of mass analyzer (or mass spectrometer) for determining the mass-to-charge ratio (m/z) of ions based on the cyclotron frequency of the ions in a fixed magnetic field.[1] The ions are trapped in a Penning trap (a magnetic field with electric trapping plates) where they are excited (at their resonant cyclotron frequencies) to a larger cyclotron radius by an oscillating electric field orthogonal to the magnetic field. After the excitation field is removed, the ions are rotating at their cyclotron frequency in phase (as a "packet" of ions). These ions induce a charge (detected as an image current) on a pair of electrodes as the packets of ions pass close to them. The resulting signal is called a free induction decay (FID), transient or interferogram that consists of a superposition of sine waves. The useful signal is extracted from this data by performing a Fourier transform to give a mass spectrum.
Contents
History
FT-ICR was invented by Melvin B. Comisarow[2] and Alan G. Marshall at the University of British Columbia. The first paper appeared in Chemical Physics Letters in 1974.[3] The inspiration was earlier developments in conventional ICR and Fourier-transform nuclear magnetic resonance (FT-NMR) spectroscopy. Marshall has continued to develop the technique at The Ohio State University and Florida State University.
Theory
The physics of FTICR is similar to that of a cyclotron at least in the first approximation.
In the simplest form (idealized) the relationship between the cyclotron frequency and the mass to charge ratio is given by:
where f = cyclotron frequency, q = ion charge, B = magnetic field strength and m = ion mass.
This is more often represented in angular frequency:
where 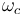 is the angular cyclotron frequency which is related to frequency by the definition
is the angular cyclotron frequency which is related to frequency by the definition 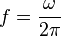 .
.
Because of the quadrupolar electrical field used to trap the ions in the axial direction this relationship is only approximate. The axial electrical trapping results in axial oscillations within the trap with the (angular) frequency:
Where 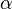 is a constant similar to the spring constant of a harmonic oscillator and is dependent on applied voltage, trap dimensions and trap geometry.
is a constant similar to the spring constant of a harmonic oscillator and is dependent on applied voltage, trap dimensions and trap geometry.
The electric field and the resulting axial harmonic motion reduces the cyclotron frequency and introduces a second radial motion called magnetron motion that occurs at the magnetron frequency. The cyclotron motion is still the frequency being used but the relationship above is not exact due to this phenomenon. The natural angular frequencies of motion are:
where 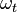 is the axial trapping frequency due the axial electrical trapping and
is the axial trapping frequency due the axial electrical trapping and  is the reduced cyclotron (angular) frequency and
is the reduced cyclotron (angular) frequency and 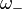 is the magnetron (angular) frequency. Again
is the magnetron (angular) frequency. Again  is what is typically measured in FTICR. The meaning of this equation can be understood qualitatively by considering the case where
is what is typically measured in FTICR. The meaning of this equation can be understood qualitatively by considering the case where 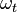 is small, which is generally true. In that case the value of the radical is just slightly less than
is small, which is generally true. In that case the value of the radical is just slightly less than 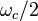 and the value of
and the value of  is just slightly less than
is just slightly less than 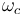 (the cyclotron frequency has been slightly reduced). For
(the cyclotron frequency has been slightly reduced). For 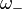 the value of the radical is the same (slightly less than
the value of the radical is the same (slightly less than 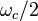 ) but it is being subtracted from
) but it is being subtracted from 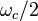 resulting in a small number equal to
resulting in a small number equal to 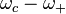 (i.e. the exact amount that the cyclotron frequency was reduced by).
(i.e. the exact amount that the cyclotron frequency was reduced by).
Instrumentation
FTICR-MS differs significantly from other mass spectrometry techniques in that the ions are not detected by hitting a detector such as an electron multiplier but only by passing near detection plates. Additionally the masses are not resolved in space or time as with other techniques but only by the ion cyclotron resonance (rotational) frequency that each ion produces as it rotates in a magnetic field. Thus, the different ions are not detected in different places as with sector instruments or at different times as with time-of-flight instruments but all ions are detected simultaneously during the detection interval. This provides an increase in the observed signal to noise ratio owing to the principles of Fellgett's advantage.[1] In FTICR-MS, resolution can be improved either by increasing the strength of the magnet (in tesla) or by increasing the detection duration.[4]
Cells
A review of different cell geometries with their specific electric configurations is available in the literature.[5] However, ICR cells can belong to one of the following two categories: closed cells or open cells.
Several closed ICR cells with different geometries were fabricated and their performance has been characterized. Grids were used as end caps to apply an axial electric field for trapping ions axially (parallel to the magnetic field lines). Ions can be either generated inside the cell or can be injected to the cell from an external ionization source. Nested ICR cells with double pair of grids were also fabricated to trap both positive and negative ions simultaneously.
The most common open cell geometry is a cylinder, which is axially segmented to produce electrodes in the shape of a ring. The central ring electrode is commonly used for applying radial excitation electric field and detection. DC electric voltage is applied on the terminal ring electrodes to trap ions along the magnetic field lines.[6] Open cylindrical cells with ring electrodes of different diameters have also been designed.[7] They proved not only capable in trapping and detecting both ion polarities simultaneously, but also they succeeded to separate positive from negative ions radially. This presented a large discrimination in kinetic ion acceleration between positive and negative ions trapped simultaneously inside the new cell. Several ion axial acceleration schemes were recently written for ion-ion collision studies [8]
Stored waveform inverse Fourier transform
Stored waveform inverse Fourier transform (SWIFT) is a method for the creation of excitation waveforms for FTMS.[9] The time-domain excitation waveform is formed from the inverse Fourier transform of the appropriate frequency-domain excitation spectrum, which is chosen to excite the resonance frequencies of selected ions. The SWIFT procedure can be used to select ions for tandem mass spectrometry experiments.
Applications
Fourier-transform ion cyclotron resonance (FTICR) mass spectrometry is a high-resolution technique that can be used to determine masses with high accuracy. Many applications of FTICR-MS use this mass accuracy to help determine the composition of molecules based on accurate mass. This is possible due to the mass defect of the elements. FTICR-MS is able to achieve higher levels of resolution than other forms of mass spectrometer, in part, because a superconducting magnet is much more stable than RF (radio frequency) voltage.[10] Another place that FTICR-MS is useful is in dealing with complex mixtures, such as biomass or waste liquefaction products,[11][12] since the resolution (narrow peak width) allows the signals of two ions with similar mass-to-charge ratios (m/z) to be detected as distinct ions.[13][14][15] This high resolution is also useful in studying large macromolecules such as proteins with multiple charges, which can be produced by electrospray ionization. For example, attomole level of detection of two peptides has been reported.[16] These large molecules contain a distribution of isotopes that produce a series of isotopic peaks. Because the isotopic peaks are close to each other on the m/z axis, due to the multiple charges, the high resolving power of the FTICR is extremely useful. FTICR-MS is very useful in other studies of proteomics as well. It achieves exceptional resolution in both top-down and bottom-up proteomics. Electron-capture dissociation (ECD), collisional-induced dissociation (CID), and infrared multiphoton dissociation (IRMPD) are all utilized to produce fragment spectra in tandem mass spectrometry experiments.[17] Although CID and IRMPD use vibrational excitation to further dissociate peptides by breaking the backbone amide linkages, which are typically low in energy and weak, CID and IRMPD may also cause dissociation of post-translational modifications. ECD, on the other hand, allows specific modifications to be preserved. This is quite useful in analyzing phosphorylation states, O- or N-linked glycosylation, and sulfating.[17]
References
- ↑ 1.0 1.1 Marshall, A. G.; Hendrickson, C. L.; Jackson, G. S., Fourier transform ion cyclotron resonance mass spectrometry: a primer. Mass Spectrom Rev 17, 1-35.
- ↑ Lua error in package.lua at line 80: module 'strict' not found.
- ↑ M.B. Comisarow and A.G. Marshall, Chem. Phys. Lett. 25, 282 (1974)
- ↑ Lua error in package.lua at line 80: module 'strict' not found.
- ↑ S. Guan, A. G. Marshall, Int. J. Mass Spectrom., 146/147 (1995) 261
- ↑ Lua error in package.lua at line 80: module 'strict' not found.
- ↑ Lua error in package.lua at line 80: module 'strict' not found.
- ↑ Lua error in package.lua at line 80: module 'strict' not found.
- ↑ Lua error in package.lua at line 80: module 'strict' not found.
- ↑ Lua error in package.lua at line 80: module 'strict' not found.
- ↑ Lua error in package.lua at line 80: module 'strict' not found.
- ↑ Lua error in package.lua at line 80: module 'strict' not found.
- ↑ Lua error in package.lua at line 80: module 'strict' not found.
- ↑ Lua error in package.lua at line 80: module 'strict' not found.
- ↑ Lua error in package.lua at line 80: module 'strict' not found.
- ↑ Lua error in package.lua at line 80: module 'strict' not found.
- ↑ 17.0 17.1 Lua error in package.lua at line 80: module 'strict' not found.
External links
- National High Field Fourier Transform Ion Cyclotron Resonance (FT-ICR) mass spectrometry facility, Tallahassee, Florida, USA
- What's in an Oil Drop? An Introduction to Fourier Transform Ion Cyclotron Resonance (FT-ICR) for Non-scientists National High Magnetic Field Laboratory
- Scottish Instrumentation Resource Centre for Advanced Mass Spectrometry
- Fourier-transform Ion Cyclotron Resonance (FT-ICR) FT-ICR Introduction University of Bristol