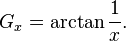Gregory number

In mathematics, a Gregory number, named after James Gregory, is a real number of the form:

$G_x = \sum_{i = 0}^\infty (-1)^i \frac{1}{(2i + 1)x^{2i + 1}}$

where x is any rational number greater or equal to 1. Considering the power series expansion for arctangent, we have

$G_x = \arctan\frac{1}{x}.$

Setting x = 1 gives the well-known Leibniz formula for pi.

See also

• Størmer number