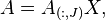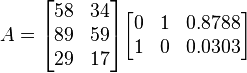Interpolative decomposition
From Infogalactic: the planetary knowledge core
In numerical analysis interpolative decomposition (ID) factors a matrix as the product of two matrices, one of which contains selected columns from the original matrix, and the other has a subset of columns that consists the identity matrix and all its values are not larger than 2 in absolute value.
Definition
Let 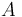 be an
be an  with rank
with rank 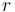 . than
. than 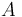 can be written as:
can be written as:
where:
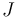 is a subset of
is a subset of 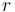 indices from
indices from 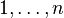
- The
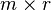 matrix
matrix 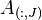 represents the
represents the 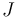 's columns of
's columns of 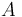
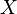 is a
is a 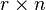 matrix that all its values are less than 2 in magnitude.
matrix that all its values are less than 2 in magnitude. 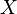 has a
has a 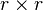 identity sub-matrix.
identity sub-matrix.
Note that similar decomposition can be done using the rows of 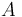 .
.
Example
Let 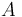 be the
be the 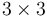 matrix of rank 2:
matrix of rank 2: 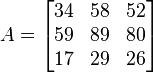
Then
There
References
- Cheng, Hongwei, Zydrunas Gimbutas, Per-Gunnar Martinsson, and Vladimir Rokhlin. "On the compression of low rank matrices." SIAM Journal on Scientific Computing 26, no. 4 (2005): 1389–1404.
- Liberty, E., Woolfe, F., Martinsson, P. G., Rokhlin, V., & Tygert, M. (2007). Randomized algorithms for the low-rank approximation of matrices. Proceedings of the National Academy of Sciences, 104(51), 20167–20172.