Zero-dimensional space

This article is about zero dimension in topology. For several kinds of zero space in algebra, see zero object (algebra).

In mathematics, a zero-dimensional topological space (or nildimensional) is a topological space that has dimension zero with respect to one of several inequivalent notions of assigning a dimension to a given topological space. An illustration of a nildimensional space is a point.

Definition

Specifically:

• A topological space is zero-dimensional with respect to the Lebesgue covering dimension if every finite open cover of the space has a finite refinement which is a cover of the space by open sets such that any point in the space is contained in exactly one open set of this refinement.
• A topological space is zero-dimensional with respect to the small inductive dimension if it has a base consisting of clopen sets.

The two notions above agree for separable, metrisable spaces.

Properties of spaces with covering dimension zero

• A zero-dimensional Hausdorff space is necessarily totally disconnected, but the converse fails. However, a locally compact Hausdorff space is zero-dimensional if and only if it is totally disconnected. (See (Arhangel'skii 2008, Proposition 3.1.7, p.136) for the non-trivial direction.)
• Zero-dimensional Polish spaces are a particularly convenient setting for descriptive set theory. Examples of such spaces include the Cantor space and Baire space.
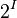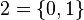• Hausdorff zero-dimensional spaces are precisely the subspaces of topological powers $2^I$ where $2=\{0,1\}$ is given the discrete topology. Such a space is sometimes called a Cantor cube. If I is countably infinite, 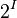$2^I$ is the Cantor space.