Rarefaction (ecology)

In ecology, rarefaction is a technique to assess species richness from the results of sampling. Rarefaction allows the calculation of species richness for a given number of individual samples, based on the construction of so-called rarefaction curves. This curve is a plot of the number of species as a function of the number of samples. On the left, the steep slope indicates that a large fraction of the species diversity remains to be discovered. If the curve becomes flatter to the right, a reasonable number of individual samples have been taken: more intensive sampling is likely to yield only few additional species.

The issue that occurs when sampling various species in a community is that the larger the number of individuals sampled, the more species that will be found. Rarefaction curves are created by randomly re-sampling the pool of N samples multiple times and then plotting the average number of species found in each sample (1,2, ... N). "Thus rarefaction generates the expected number of species in a small collection of n individuals (or n samples) drawn at random from the large pool of N samples.". Rarefaction curves generally grow rapidly at first, as the most common species are found, but the curves plateau as only the rarest species remain to be sampled.

A set of rarefaction curves from a NASA biology study

History

The technique of rarefaction was developed in 1968 by Howard Sanders in a biodiversity assay of marine benthic ecosystems, as he sought a model for diversity that would allow him to compare species richness data among sets with different sample sizes; he developed rarefaction curves as a method to compare the shape of a curve rather than absolute numbers of species.

Following initial development by Sanders, the technique of rarefaction has undergone a number of revisions. In a paper criticizing many methods of assaying biodiversity, Stuart Hurlbert refined the problem that he saw with Sanders' rarefaction method, that it overestimated the number of species based on sample size, and attempted to refine his methods. The issue of overestimation was also dealt with by Daniel Simberloff, while other improvements in rarefaction as a statistical technique were made by Ken Heck in 1975.

Today, rarefaction has grown as a technique not just for measuring species diversity, but of understanding diversity at higher taxonomic levels as well. Most commonly, the number of species is sampled to predict the number of genera in a particular community; similar techniques had been used to determine this level of diversity in studies several years before Sanders quantified his individual to species determination of rarefaction. Rarefaction techniques are used to quantify species diversity of newly studied ecosystems, as well as in applied studies in community ecology, such as understanding pollution impacts on communities and other management applications.

Derivation

Deriving Rarefaction:
N = total number of items
K = total number of groups
N_i = the number of items in group i (i = 1, ..., K).
M_j = number of groups consisting in j elements

From these definitions, it therefore follows that:

$\sum_{i=1}^K N_i = N$
$\sum_{j=1}^{\infin} M_j = K$
$\sum_{j=1}^{\infin} jM_j = N$

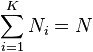
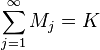
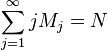
In a rarefied sample we have chosen a random subsample n from the total N items. The relevance of a rarefied sample is that some groups may now be necessarily absent from this subsample. We therefore let:

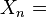$X_n =$the number of groups still present in the subsample of "n" items
It is true that 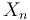$X_n$ is less than K whenever at least one group is missing from this subsample.

Therefore the rarefaction curve, 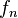$f_n$ is defined as:

$f_n = E[X_n] = K - \binom{N}{n}^{-1} \sum_{i=1}^K {\binom{N-N_i}{n}}$

From this it follows that 0 ≤ f(n) ≤ K. Furthermore, 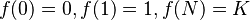$f(0)= 0, f(1) = 1, f(N) = K$. Despite being defined at discrete values of n, these curves are most frequently displayed as continuous functions.

Correct usage

Rarefaction curves are necessary for estimating species richness. Raw species richness counts, which are used to create accumulation curves, can only be compared when the species richness has reached a clear asymptote. Rarefaction curves produce smoother lines that facilitate point-to-point or full dataset comparisons.

One can plot the number of species as a function of either the number of individuals sampled or the number of samples taken. The sample-based approach accounts for patchiness in the data that results from natural levels of sample heterogeneity. However, when sample-based rarefaction curves are used to compare taxon richness at comparable levels of sampling effort, the number of taxa should be plotted as a function of the accumulated number of individuals, not accumulated number of samples, because datasets may differ systematically in the mean number of individuals per sample.

One cannot simply divide the number of species found by the number of individuals sampled in order to correct for different sample sizes. Doing so would assume that the number of species increases linearly with the number of individuals present, which is not always true.

Rarefaction analysis assumes that the individuals in an environment are randomly distributed, the sample size is sufficiently large, that the samples are taxonomically similar, and that all of the samples have been performed in the same manner. If these assumptions are not met, the resulting curves will be greatly skewed.

Cautions and criticism

Rarefaction only works well when no taxon is extremely rare or common(Ref. needed), or when beta diversity is very high. Rarefaction assumes that the number of occurrences of a species reflects the sampling intensity, but if one taxon is especially common or rare, the number of occurrences will be related to the extremity of the number of individuals of that species, not to the intensity of sampling.

The technique does not account for specific taxa. It examines the number of species present in a given sample, but does not look at which species are represented across samples. Thus, two samples that each contain 20 species may have completely different compositions, leading to a skewed estimate of species richness.

The technique does not recognize species abundance, only species richness. A true measure of diversity accounts for both the number of species present and the relative abundance of each.

Rarefaction is unrealistic in its assumption of random spatial distribution of individuals.

Rarefaction does not provide an estimate of asymptotic richness, so it cannot be used to extrapolate species richness trends in larger samples.

External links

• Rarefaction Calculator
• EcoSim Professional Rarefaction Software
• PAST (PAlaeontological STatistics)