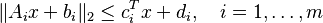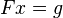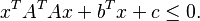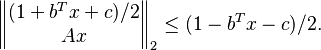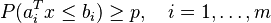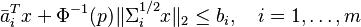Second-order cone programming
Lua error in package.lua at line 80: module 'strict' not found.
A second-order cone program (SOCP) is a convex optimization problem of the form
- minimize
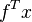
- subject to
where the problem parameters are 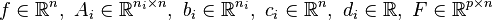 , and
, and 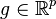 . Here
. Here 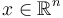 is the optimization variable. [1] When
is the optimization variable. [1] When  for
for 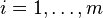 , the SOCP reduces to a linear program. When
, the SOCP reduces to a linear program. When 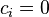 for
for 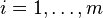 , the SOCP is equivalent to a convex quadratically constrained linear program. Quadratically constrained quadratic programs can also be formulated as SOCPs by reformulating the objective function as a constraint. Semidefinite programming subsumes SOCPs as the SOCP constraints can be written as linear matrix inequalities (LMI) and can be reformulated as an instance of semi definite program. SOCPs can be solved with great efficiency by interior point methods.
, the SOCP is equivalent to a convex quadratically constrained linear program. Quadratically constrained quadratic programs can also be formulated as SOCPs by reformulating the objective function as a constraint. Semidefinite programming subsumes SOCPs as the SOCP constraints can be written as linear matrix inequalities (LMI) and can be reformulated as an instance of semi definite program. SOCPs can be solved with great efficiency by interior point methods.
Contents
Example: Quadratic constraint
Consider a quadratic constraint of the form
This is equivalent to the SOC constraint
Example: Stochastic linear programming
Consider a stochastic linear program in inequality form
- minimize
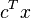
- subject to
where the parameters 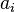 are independent Gaussian random vectors with mean
are independent Gaussian random vectors with mean  and covariance
and covariance 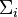 and
and 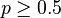 . This problem can be expressed as the SOCP
. This problem can be expressed as the SOCP
- minimize
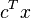
- subject to
where 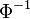 is the inverse normal cumulative distribution function.[1]
is the inverse normal cumulative distribution function.[1]
Example: Stochastic second-order cone programming
We refer to second-order cone programs as deterministic second-order cone programs since data defining them are deterministic. Stochastic second-order cone programs[2] is a class of optimization problems that defined to handle uncertainty in data defining deterministic second-order cone programs.
Solvers and scripting (programming) languages
| Name | License | Brief info |
|---|---|---|
| AMPL | commercial | An algebraic modeling language with SOCP support |
| CPLEX | commercial | |
| ECOS | GPL v3 | SOCP solver for embedded applications |
| Gurobi | commercial | parallel SOCP barrier algorithm |
| JOptimizer | Apache License | Java library for convex optimization (open source) |
| MOSEK | commercial | |
| OpenOpt | BSD | universal cross-platform numerical optimization framework, see its SOCP page and other problems involved. Uses NumPy arrays and SciPy sparse matrices. |
| SCS | MIT License | C library that solves large-scale convex cone problems |
| SDPT3 | GPL v2 | Matlab package with primal–dual interior point methods[3][2][4][5][6] |
| Xpress | commercial | from 7.6 release |
References
- ↑ 1.0 1.1 Lua error in package.lua at line 80: module 'strict' not found.
- ↑ 2.0 2.1 Lua error in package.lua at line 80: module 'strict' not found.
- ↑ Lua error in package.lua at line 80: module 'strict' not found.
- ↑ Lua error in package.lua at line 80: module 'strict' not found.
- ↑ |SeDuMi||GPL v3||Matlab package with primal–dual interior point methods
- ↑ Lua error in package.lua at line 80: module 'strict' not found.