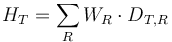Sievert

For other uses, see Sievert (disambiguation).

Sievert
Unit system	SI derived unit
Unit of	Health effect of ionizing radiation
Symbol	Sv
Named after	Rolf Maximilian Sievert
Unit conversions
1 Sv in ...	... is equal to ...
SI base units	m2⋅s-2
Energy absorbed by mass	J⋅kg-1

The sievert (symbol: Sv) is a derived unit of ionizing radiation dose in the International System of Units (SI). It is a measure of the health effect of low levels of ionizing radiation on the human body.

Quantities that are measured in sieverts are intended to represent the stochastic health risk, which for radiation dose assessment is defined as the probability of cancer induction and genetic damage.

The sievert is used for radiation dose quantities such as equivalent dose, effective dose, and committed dose. It is used both to represent the risk of the effect of external radiation from sources outside the body, and the effect of internal irradiation due to inhaled or ingested radioactive substances.

Conventionally the sievert is not used for high dose rates of radiation which produce deterministic effects, which is the severity of acute tissue damage which is certain to happen. These effects are compared to the physical quantity absorbed dose measured by the unit gray (Gy).

To enable consideration of stochastic health risk, calculations are performed to convert the physical quantity absorbed dose into equivalent and effective doses, the details of which depend on the radiation type and biological context. For applications in radiation protection and dosimetry assessment the International Commission on Radiological Protection (ICRP) and International Commission on Radiation Units and Measurements (ICRU) have published recommendations and data which are used to calculate these.

The sievert is of fundamental importance in dosimetry and radiation protection, and is named after Rolf Maximilian Sievert, a Swedish medical physicist renowned for work on radiation dosage measurement and research into the biological effects of radiation. One sievert carries with it a 5.5% chance of eventually developing cancer.

One sievert equals 100 rem. The rem is an older, non-SI unit of measurement.

To enable a comprehensive view of the sievert this article deals with the definition of the sievert as an SI unit, summarises the recommendations of the ICRU and ICRP on how the sievert is calculated, includes a guide to the effects of ionizing radiation as measured in sieverts, and gives examples of approximate figures of dose uptake in certain situations.

Definition

CIPM definition of the sievert

The SI definition given by the International Committee for Weights and Measures (CIPM) says:

"The quantity dose equivalent H is the product of the absorbed dose D of ionizing radiation and the dimensionless factor Q (quality factor) defined as a function of linear energy transfer by the ICRU"

H = Q × D

The value of Q is not defined further by CIPM, but it requires the use of the relevant ICRU and ICRP recommendations to provide this value.

The CIPM also says that "in order to avoid any risk of confusion between the absorbed dose D and the dose equivalent H, the special names for the respective units should be used, that is, the name gray should be used instead of joules per kilogram for the unit of absorbed dose D and the name sievert instead of joules per kilogram for the unit of dose equivalent H".

In summary:

The gray - quantity "D"

1 Gy = 1 joule/kilogram - a physical quantity. 1 Gy is the deposit of a joule of radiation energy in a kg of matter or tissue.

The sievert - quantity "H"

1 Sv = 1 joule/kilogram - a biological effect. The sievert represents the equivalent biological effect of the deposit of a joule of radiation energy in a kilogram of human tissue. The equivalence to absorbed dose is denoted by Q.

ICRP definition of the sievert

The ICRP definition of the sievert is; "The sievert is the special name for the SI unit of equivalent dose, effective dose, and operational dose quantities. The unit is joule per kilogram".

The sievert is used for a number of dose quantities which are described in this article and are part of the international radiological protection system devised and defined by the ICRP and ICRU.

Naming conventions - These dose quantities have specific purposes and meanings, but there can be confusion between, for instance, equivalent dose and dose equivalent. Although the CIPM definition states that the linear energy transfer function (Q) of the ICRU is used in calculating the biological effect, the ICRP in 1990 developed the "protection" dose quantities effective and equivalent dose which are calculated from more complex computational models and are distinguished by not having the phrase dose equivalent in their name. Only the operational dose quantities which use Q for calculation, retain this phrase. In the USA there are differently named dose quantities which are not part of the ICRP system.

External dose quantities

External radiation dose quantities used in radiological protection

The sievert is used to represent the biological effects of different forms of external ionizing radiation on various types of human tissue. Some quantities cannot be practically measured, but they must be related to actual instrumentation and dosimetry measurements. The resultant complexity has required the creation of a number of different dose quantities within a coherent system developed by the ICRU working with the ICRP. The external dose quantities and their relationships are shown in the accompanying diagram.

Physical quantities

These are directly measurable physical quantities in which no allowance has been made for biological effects. Radiation fluence is the number of radiation particles impinging per unit area per unit time, kerma is the ionising effect of the radiation field, and absorbed dose is the amount of radiation energy deposited per unit mass.

Protection quantities

The protection quantities are used as "limiting quantities" to specify exposure limits to ensure, in the words of ICRP, that the occurrence of stochastic health effects is kept below unacceptable levels and that tissue reactions are avoided. However, these quantities cannot be practically measured and are a calculated value of dose of organs of the human body, which is arrived at by using anthropomorphic phantoms. These are 3D computational models of the human body which take into account a number of complex effects such as body self-shielding and internal scattering of radiation.

As protection quantities cannot practically be measured, operational quantities are used to relate them to practical radiation instrument and dosimeter responses.

Operational quantities

Operational quantities provide an estimate or upper limit for the value of the protection quantities related to an exposure, and are used in practical regulations or guidance. They relate radiological instrument measurements to the calculated protection quantities.

The calibration of individual and area dosemeters in photon fields is performed by measuring the collision "air kerma free in air" under conditions of secondary electron equilibrium. Then the appropriate operational quantity is derived applying a conversion coefficient that relates the air kerma to the appropriate operational quantity. The conversion coefficients for photon radiation are published by the ICRU.

Simple (non-anthropomorphic) "phantoms" are used to relate operational quantities to measured free-air irradiation. The ICRU sphere phantom is based on the definition of an ICRU 4-element tissue-equivalent material which does not really exist and cannot be fabricated. The ICRU sphere is a theoretical 30 cm diameter "tissue equivalent" sphere consisting of a material with a density of 1 g·cm⁻³ and a mass composition of 76.2% oxygen, 11.1% carbon, 10.1% hydrogen and 2.6% nitrogen. This material is specified to most closely approximate human tissue in its absorption properties. According to the ICRP, the ICRU "sphere phantom" in most cases adequately approximates the human body as regards the scattering and attenuation of penetrating radiation fields under consideration. Thus radiation of a particular energy fluence will have roughly the same energy deposition within the sphere as it would in the equivalent mass of human tissue.

To allow for back-scattering and absorption of the human body, the "slab phantom" is used to represent the human torso for practical calibration of whole body dosimeters. The slab phantom is 300 mm × 300 mm × 150 mm depth to represent the human torso.

Instrument and dosimetry response

This is an actual reading obtained from such as an ambient dose gamma monitor, or a personal dosimeter.

Calculating protection dose quantities

Relationships of SI external "protection" dose quantities

The sievert is used in external radiation protection when discussing equivalent dose (the external-source, whole-body exposure effects, in a uniform field), and effective dose (which depends on the body parts irradiated). These dose quantities are weighted averages of absorbed dose designed to be representative of the stochastic health effects of radiation, and use of the sievert implies that appropriate weighting factors have been applied to the absorbed dose measurement or calculation (expressed in grays).

The ICRP calculation provides two weighting factors to enable the calculation of protection quantities.

 1. The radiation factor W_R, which is specific for radiation type R - This is used in calculating the equivalent dose H_T which can be for the whole body or for individual organs.

 2. The tissue weighting factor W_T, which is specific for tissue type T being irradiated. This is used with W_R to calculate the contributory organ doses to arrive at an effective dose E for non-uniform irradiation.

When a whole body is irradiated uniformly only the radiation weighting factor W_R is used, and the effective dose equals the whole body equivalent dose. But if the irradiation of a body is partial or non-uniform the tissue factor W_T is used to calculate dose to each organ or tissue. These are then summed to obtain the effective dose. In the case of uniform irradiation of the human body, these summate to 1, but in the case of partial or non-uniform irradiation, they will summate to a lower value depending on the organs concerned; reflecting the lower overall health effect. The calculation process is shown on the accompanying diagram. This approach calculates the biological risk contribution to the whole body, taking into account complete or partial irradiation, and the radiation type or types. The values of these weighting factors are conservatively chosen to be greater than the bulk of experimental values observed for the most sensitive cell types, based on averages of those obtained for the human population.

Radiation type weighting factor W_R

Main article: equivalent dose

As various radiation types have different biological effects for the same deposited energy, a corrective radiation weighting factor Wr, is applied to convert the absorbed dose measured in the unit gray, into the equivalent dose measured in the unit sievert. Wr, which is dependent on the radiation type irradiating the target tissue.

Radiation weighting factors W_R
used to represent relative biological effectiveness
according to ICRP report 103

Radiation	Energy	WR (formerly Q)
x-rays, gamma rays, beta particles, muons		1
neutrons	< 1 MeV	2.5 + 18.2·e−[ln(E)]²/6
	1 MeV - 50 MeV	5.0 + 17.0·e−[ln(2·E)]²/6
	> 50 MeV	2.5 + 3.25·e−[ln(0.04·E)]²/6
protons, charged pions		2
alpha particles, Nuclear fission products, heavy nuclei		20

The equivalent dose is calculated by multiplying the absorbed energy, averaged by mass over an organ or tissue of interest, by a radiation weighting factor appropriate to the type and energy of radiation. To obtain the equivalent dose for a mix of radiation types and energies, a sum is taken over all types of radiation energy dose.

$H_T = \sum_R W_R \cdot D_{T,R}\$

where

H_T is the equivalent dose absorbed by tissue T

D_T,R is the absorbed dose in tissue T by radiation type R

W_R is the radiation weighting factor defined by regulation

Thus for example, an absorbed dose of 1 Gy by alpha particles will lead to an equivalent dose of 20 Sv.

The radiation weighting factor for neutrons has been revised over time and remains controversial.

This may appear to lead to a paradox, as this would suggest that the energy of the incident radiation field in joules has increased by a factor of 20, thereby violating the laws of Conservation of energy. However this is not the case, the sievert is used only to convey the fact that the biological effect of absorbing a gray of alpha particles would result in a 20 fold increase in the amount of biological effects that one would observe by absorbing a gray of x-rays. It is this biological component that is being expressed when using sieverts rather than the actual physical energy delivered by the incident absorbed radiation.

Tissue type weighting factor W_T

Main article: effective dose (radiation)

The second weighting factor is the tissue factor W_T, but it is used only if there is has been non-uniform irradiation of a body. If the body has been subject to uniform irradiation, the effective dose equals the whole body equivalent dose, and only the radiation weighting factor W_R is used. But if there is partial or non-uniform body irradiation the calculation must take account of the individual organ doses received, because the sensitivity of each organ to irradiation depends on their tissue type. This summed dose from only those organs concerned gives the effective dose for the whole body. The tissue weighting factor is used to calculate those individual organ dose contributions.

The ICRP values for W_T are given in the table shown here.

Weighting factors for different organs

Organs	Tissue weighting factors
	ICRP26 1977	ICRP60 1990	ICRP103 2007
Gonads	0.25	0.20	0.08
Red Bone Marrow	0.12	0.12	0.12
Colon	-	0.12	0.12
Lung	0.12	0.12	0.12
Stomach	-	0.12	0.12
Breasts	0.15	0.05	0.12
Bladder	-	0.05	0.04
Liver	-	0.05	0.04
Oesophagus	-	0.05	0.04
Thyroid	0.03	0.05	0.04
Skin	-	0.01	0.01
Bone surface	0.03	0.01	0.01
Salivary glands	-	-	0.01
Brain	-	-	0.01
Remainder of body	0.30	0.05	0.12
Total	1.00	1.00	1.00

The article on effective dose gives the method of calculation. The absorbed dose is first corrected for the radiation type to give the equivalent dose, and then corrected for the tissue receiving the radiation. Some tissues like bone marrow are particularly sensitive to radiation, so they are given a weighting factor that is disproportionally large relative to the fraction of body mass they represent. Other tissues like the hard bone surface are particularly insensitive to radiation and are assigned a disproportionally low weighting factor.

In summary, the sum of tissue-weighted doses to each irradiated organ or tissue of the body adds up to the effective dose for the body. The use of effective dose enables comparisons of overall dose received regardless of the extent of body irradiation.

Operational quantities

The operational quantities are used in practical applications for monitoring and investigating external exposure situations. They are defined for practical operational measurements and assessment of doses in the body. Three external operational dose quantities were devised to relate operational dosimeter and instrument measurements to the calculated protection quantities. Also devised were two phantoms, The ICRU "slab" and "sphere" phantoms which relate these quantities to incident radiation quantities using the Q(L) calculation.

Ambient dose equivalent

This is used for area monitoring of penetrating radiation and is usually expressed as the quantity H*(10). This means the radiation is equivalent to that found 10 mm within the ICRU sphere phantom in the direction of origin of the field. An example of penetrating radiation is Gamma rays.

Directional dose equivalent

This is used for monitoring of low penetrating radiation and is usually expressed as the quantity H'(0.07). This means the radiation is equivalent to that found at a depth of 0.07 mm in the ICRU sphere phantom. Examples of low penetrating radiation are alpha particles, beta particles and low-energy photons. This dose quantity is used for the determination of equivalent dose to such as the skin, lens of the eye. In radiological protection practice value of omega is usually not specified as the dose is usually at a maximum at the point of interest.

Personal dose equivalent

This is used for individual dose monitoring, such as with a personal dosimeter worn on the body. The recommended depth for assessment is 10 mm which gives the quantity H_p(10).

Internal dose quantities

Main article: Committed dose

The sievert is used for human internal dose quantities in calculating committed dose. This is dose from radionuclides which have been ingested or inhaled into the human body, and thereby "committed" to irradiate the body for a period of time. The concepts of calculating protection quantities as described for external radiation applies, but as the source of radiation is within the tissue of the body, the calculation of absorbed organ dose uses different coefficients and irradiation mechanisms.

The ICRP defines Committed effective dose, E(t) as the sum of the products of the committed organ or tissue equivalent doses and the appropriate tissue weighting factors W_T, where t is the integration time in years following the intake. The commitment period is taken to be 50 years for adults, and to age 70 years for children.

The ICRP further states "For internal exposure, committed effective doses are generally determined from an assessment of the intakes of radionuclides from bioassay measurements or other quantities (e.g., activity retained in the body or in daily excreta). The radiation dose is determined from the intake using recommended dose coefficients".

A committed dose from an internal source is intended to carry the same effective risk as the same amount of equivalent dose applied uniformly to the whole body from an external source, or the same amount of effective dose applied to part of the body.

Health effects

Ionizing radiation has deterministic and stochastic effects on human health. Deterministic (acute tissue effect) events happen with certainty, with the resulting health conditions occurring in every individual who received the same high dose. Stochastic (cancer induction and genetic) events are inherently random, with most individuals in a group, failing to ever exhibit any causal negative health effects after exposure, while an indeterministic random minority do, often with the resulting subtle negative health effects being observable only after large detailed epidemiology studies.

The use of the sievert implies that only stochastic effects are being considered, and to avoid confusion deterministic effects are conventionally compared to values of absorbed dose expressed by the SI unit gray (Gy).

Stochastic effects

Stochastic effects are those that occur randomly, such as radiation-induced cancer. The consensus of nuclear regulators, the nuclear industry, governments, some Academy of Sciences and the UNSCEAR, is that the incidence of cancers due to ionizing radiation can be modeled as increasing linearly with effective dose at a rate of 5.5% per sievert. This is known as the Linear no-threshold model. Individual studies, alternative models, and earlier versions of the industry consensus have produced other risk estimates scattered around this consensus model. There is general agreement that the risk is much higher for infants and fetuses than adults, higher for the middle-aged than for seniors, and higher for women than for men, though there is no quantitative consensus about this.

Deterministic effects

The deterministic (acute tissue damage) effects that can lead to acute radiation syndrome only occur in the case of acute high doses (> ~0.1 Gy) and high dose rates (> ~0.1 Gy/h) and are conventionally not measured using the unit sievert, but use the unit gray (Gy). A model of deterministic risk would require different weighting factors (not yet established) than are used in the calculation of equivalent and effective dose.

ICRP dose limits

The International Commission on Radiological Protection recommends limiting artificial irradiation. For occupational exposure, the limit is 50 mSv in a single year with a maximum of 100 mSv in a consecutive five-year period, and for the public to an average of 1 mSv (0.001 Sv) of effective dose per year, not including medical and occupational exposures.

For comparison, natural radiation levels inside the US capitol building are such that a human body would receive an additional dose rate of 0.85 mSv/a, close to the regulatory limit, because of the uranium content of the granite structure. According to the conservative ICRP model, someone who spent 20 years inside the capitol building would have an extra one in a thousand chance of getting cancer, over and above any other existing risk. (calculated as: 20 a·0.85 mSv/a·0.001 Sv/mSv·5.5%/Sv = ~0.1%). However, that "existing risk" is much higher; an average American would have a 10% chance of getting cancer during this same 20-year period, even without any exposure to artificial radiation (See natural Epidemiology of cancer and cancer rates). These estimates are, however, unmindful of every living cell's natural repair mechanisms, evolved over a few billion years of exposure to environmental chemical and radiation threats that were higher in the past, and exaggerated by the evolution of oxygen metabolism.

Dose examples

Main article: Orders of magnitude (radiation)

Various doses of radiation in sieverts, ranging from trivial to lethal.

Comparison of radiation doses - includes the amount detected on the trip from Earth to Mars by the RAD on the MSL (2011–2013).

Significant radiation doses are not frequently encountered in everyday life, the following examples can help illustrate relative magnitudes. These are meant to be examples only, not a comprehensive list of possible radiation doses. An "acute dose" is one that occurs over a short and finite period of time, while a "chronic dose" is a dose that continues for an extended period of time so that it is better described by a dose rate.

Dose examples

0.098	μSv:	banana equivalent dose, a whimsical unit of radiation dose representing the measure of radiation from a typical banana
0.25	μSv:	U.S. limit on effective dose from a single airport security screening
5 to 10	μSv:	one set of dental radiographs
80	μSv:	average dose to people living within 16 km of Three Mile Island accident
0.4 to 0.6	mSv:	two-view mammogram, using weighting factors updated in 2007
1	mSv:	The U.S. 10 CFR § 20.1301(a)(1) dose limit for individual members of the public, total effective dose equivalent, per annum
1.5 to 1.7	mSv:	annual dose for flight attendants
2 to 7	mSv:	barium fluoroscopy, e.g. Barium meal, up to 2 minutes, 4–24 spot images
10 to 30	mSv:	single full-body CT scan
50	mSv:	The U.S. 10 C.F.R. § 20.1201(a)(1)(i) occupational dose limit, total effective dose equivalent, per annum
68	mSv:	estimated maximum dose to evacuees who lived closest to the Fukushima I nuclear accidents
80	mSv:	6 months stay on the International Space Station
250	mSv:	6-month trip to Mars - radiation due to cosmic rays, which are very difficult to shield against
500	mSv:	The U.S. 10 C.F.R. § 20.1201(a)(2)(ii) occupational dose limit, shallow-dose equivalent to skin, per annum
670	mSv:	highest dose received by a worker responding to the Fukushima emergency
1	Sv:	Maximum allowed radiation exposure for NASA astronauts over their career
4.5 to 6	Sv:	fatal acute doses during Goiânia accident
5.1	Sv:	fatal acute dose to Harry Daghlian in 1945 criticality accident
21	Sv:	fatal acute dose to Louis Slotin in 1946 criticality accident
54	Sv:	fatal acute dose to Boris Korchilov in 1961 after a reactor cooling system failed on the Soviet submarine K-19 which required work in the reactor with no shielding
64	Sv:	nonfatal dose to Albert Stevens spread over ~21 years, due to a 1945 plutonium injection experiment by doctors working on the secret Manhattan Project.

Dose rate examples

All conversions between hours and years have assumed continuous presence in a steady field, disregarding known fluctuations, intermittent exposure and radioactive decay. Converted values are shown in parentheses.

<1	mSv/a	<0.1	μSv/h	Steady dose rates below 0.1 µSv/h are difficult to measure.
1	mSv/a	(0.1	μSv/h avg)	ICRP recommended maximum for external irradiation of the human body, excluding medical and occupational exposures.
2.4	mSv/a	(0.27	μSv/h avg)	Human exposure to natural background radiation, global average
24	mSv/a	(2.7	μSv/h avg)	Natural background radiation at airline cruise altitude
130	mSv/a	(15	μSv/h avg)	Ambient field inside most radioactive house in Ramsar, Iran
(800	mSv/a)	90	μSv/h	Natural radiation on a monazite beach near Guarapari, Brazil.
(9	Sv/a)	1	mSv/h	NRC definition of a high radiation area in a nuclear power plant, warranting a chain-link fence
(240	Sv/a)	27	mSv/h	close proximity to a 100 W radioisotope thermal generator
(1.7	kSv/a)	190	mSv/h	Highest reading from fallout of the Trinity bomb, 32 km away, 3 hours after detonation.
(>90	kSv/a)	>10	Sv/h	most radioactive hotspot found in Fukushima I in areas normally accessible to workers
(2.3	MSv/a)	270	Sv/h	typical PWR spent fuel bundle, after 10 year cooldown, no shielding
(90	MGy/a)	10	kGy/h	Immediate predicted activation of reactor wall in possible future fusion reactors. After 100 years of decay, typical levels would be 2–20 mSv/h. After approximately 300 years of decay the fusion waste would produce the same dose rate as exposure to coal ash, with the volume of fusion waste naturally being orders of magnitude less than from coal ash.

Notes on examples:

History

The sievert has its origin in the roentgen equivalent man (rem) which was derived from CGS units. The International Commission on Radiation Units and Measurements (ICRU) promoted a switch to coherent SI units in the 1970s, and announced in 1976 that it planned to formulate a suitable unit for equivalent dose. The ICRP pre-empted the ICRU by introducing the sievert in 1977.

The sievert was adopted by the International Committee for Weights and Measures (CIPM) in 1980, five years after adopting the gray. The CIPM then issued an explanation in 1984, recommending when the sievert should be used as opposed to the gray. That explanation was updated in 2002 to bring it closer to the ICRP's definition of equivalent dose, which had changed in 1990. Specifically, the ICRP had introduced equivalent dose, renamed the quality factor (Q) to radiation weighting factor (W_R), and dropped another weighting factor 'N' in 1990. In 2002, the CIPM similarly dropped the weighting factor 'N' from their explanation but otherwise kept other old terminology and symbols. This explanation only appears in the appendix to the SI brochure and is not part of the definition of the sievert.

Common SI usage

This SI unit is named after Rolf Maximilian Sievert. As with every International System of Units (SI) unit named for a person, the first letter of its symbol is upper case (Sv). However, when an SI unit is spelled out in English, it should always begin with a lower case letter (sievert)—except in a situation where any word in that position would be capitalized, such as at the beginning of a sentence or in material using title case. Note that "degree Celsius" conforms to this rule because the "d" is lowercase.— Based on The International System of Units, section 5.2.

Frequently used SI prefixes are the millisievert (1 mSv = 0.001 Sv) and microsievert (1 μSv = 0.000001 Sv) and commonly used units for time derivative or "dose rate" indications on instruments and warnings for radiological protection are μSv/h and mSv/h. Regulatory limits and chronic doses are often given in units of mSv/a or Sv/a, where they are understood to represent an average over the entire year. In many occupational scenarios, the hourly dose rate might fluctuate to levels thousands of times higher for a brief period of time, without infringing on the annual limits. The conversion from hours to years varies because of leap years and exposure schedules, but approximate conversions are:

1 mSv/h = 8.766 Sv/a

114.1 μSv/h = 1 Sv/a

Conversion from hourly rates to annual rates is further complicated by seasonal fluctuations in natural radiation, decay of artificial sources, and intermittent proximity between humans and sources. The ICRP once adopted fixed conversion for occupational exposure, although these have not appeared in recent documents:

8 h = 1 day

40 h = 1 week

50 weeks = 1 year

Therefore, for occupation exposures of that time period,

1 mSv/h = 2 Sv/a

500 µSv/h = 1 Sv/a

Radiation-related quantities

Graphic showing relationships between radioactivity and detected ionizing radiation

The following table shows radiation quantities in SI and non-SI units.

Quantity	Name	Symbol	Unit	Year	System
Exposure (X)	röntgen	R	esu / 0.001293 g of air	1928	non-SI
Absorbed dose (D)			erg•g−1	1950	non-SI
	rad	rad	100 erg•g−1	1953	non-SI
	gray	Gy	J•kg−1	1974	SI
Activity (A)	curie	Ci	3.7 × 1010 s−1	1953	non-SI
	becquerel	Bq	s−1	1974	SI
Dose equivalent (H)	röntgen equivalent man	rem	100 erg•g−1	1971	non-SI
	sievert	Sv	J•kg−1	1977	SI
Fluence (Φ)	(reciprocal area)		cm−2 or m−2	1962	SI (m−2)

Although the United States Nuclear Regulatory Commission permits the use of the units curie, rad, and rem alongside SI units, the European Union European units of measurement directives required that their use for "public health ... purposes" be phased out by 31 December 1985.

Rem equivalence

An older unit for the dose equivalent is the rem, still often used in the United States. One sievert is equal to 100 rem:

100.0000 rem	=	100,000.0 mrem	=	1 Sv	=	1.000000 Sv	=	1000.000 mSv	=	1,000,000 µSv
1.0000 rem	=	1000.0 mrem	=	1 rem	=	0.010000 Sv	=	10.000 mSv	=	10000 µSv
0.1000 rem	=	100.0 mrem	=	1 mSv	=	0.001000 Sv	=	1.000 mSv	=	1000 µSv
0.0010 rem	=	1.0 mrem	=	1 mrem	=	0.000010 Sv	=	0.010 mSv	=	10 µSv
0.0001 rem	=	0.1 mrem	=	1 µSv	=	0.000001 Sv	=	0.001 mSv	=	1 µSv

See also

• Becquerel (disintegrations per second)
• Counts per minute
• Rutherford (unit)
• Sverdrup (a non-SI unit of volume transport with the same symbol Sv as sievert)

External links

• Eurados - The European radiation dosimetry group