データマイニング勉強会3
- 1. 機械学習入門 – SVMによる画像分類 yokkuns: 里 洋平 第3回 データマイニング+WEB 勉強会
- 2. 機械学習入門 – SVMによる画像分類 yokkuns: 里 洋平 第3回 データマイニング+WEB 勉強会
- 3. AGENDA 自己紹介 機械学習 SVM マージンの最大化 カーネル関数を用いた柔軟なモデリング ハードマージンとソフトマージン ラグランジュ乗数 パラメータ推定の定式化 RによるSVMの使用例
- 4. 自己紹介 id : yokkuns 名前 : 里 洋平 職業 : Webエンジニア 出身 : 種子島 趣味 : プログラミングとかカラオケとか 主催してる勉強会 : Tokyo.R、数式ニヤニヤ勉強会 統計とか機械学習やりはじめたのは割と最近なので 、 突っ込み大歓迎です!
- 5. 機械学習とは
- 6. 機械学習とは 人間が自然に行っている学習能力と同じ機能をコン ピュータで実現させる技術・手法 サンプルデータを対象に解析を行い、そのデータか ら有用な規則、ルールなどを抽出 大きく以下のように分類出来る 教師あり学習 教師なし学習 強化学習
- 7. 記憶ベース推論 車
- 8. 記憶ベース推論 テレビ
- 9. 記憶ベース推論 ギター
- 10. 記憶ベース推論 車 今までの経験・記憶がベースとなって 判断している! ギター テレビ
- 11. コンピュータにやらせる! 車 学習データ 特徴を抽出して、 学習データと比較! ギター テレビ
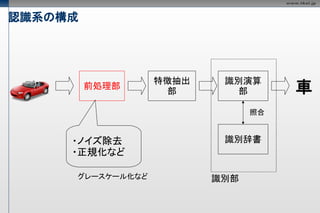
- 12. 認識系の構成 特徴抽出 識別演算 前処理部 部 部 車 照合 識別辞書 識別部
- 13. 認識系の構成 特徴抽出 識別演算 前処理部 部 部 車 照合 ・ノイズ除去 識別辞書 ・正規化など グレースケール化など 識別部
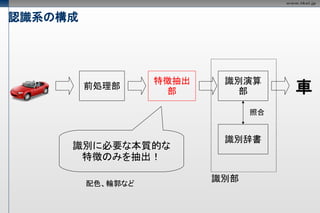
- 14. 認識系の構成 特徴抽出 識別演算 前処理部 部 部 車 照合 識別辞書 識別に必要な本質的な 特徴のみを抽出! 配色、輪郭など 識別部
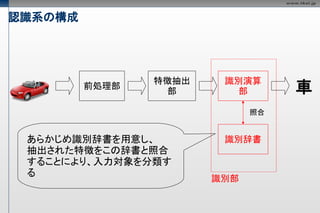
- 15. 認識系の構成 特徴抽出 識別演算 前処理部 部 部 車 照合 あらかじめ識別辞書を用意し、 識別辞書 抽出された特徴をこの辞書と照合 することにより、入力対象を分類す る 識別部
- 16. サポートベクターマシン(SVM)
- 17. サポートベクターマシン 実データの解析に広く利用されている判別手法 特徴 マージン最大化を基準とすることで、高い判別性能を実 現 カーネル関数を用いた柔軟なモデリング パラメータ推定が凸2次最適化問題として定式化されるた め、高速な最適化アルゴリズムが利用可能
- 18. サポートベクターマシン 実データの解析に広く利用されている判別手法 特徴 マージン最大化を基準とすることで、高い判別性能を実 現 カーネル関数を用いた柔軟なモデリング パラメータ推定が凸2次最適化問題として定式化されるた め、高速な最適化アルゴリズムが利用可能
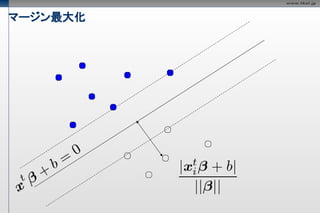
- 19. マージン最大化
- 20. マージン最適化
- 21. マージン最大化
- 22. マージン最大化
- 23. マージン最大化
- 24. マージン最大化
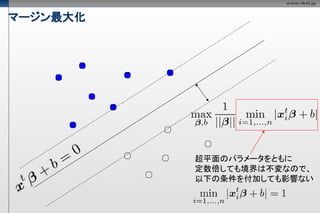
- 25. マージン最大化 超平面のパラメータをともに 定数倍しても境界は不変なので、 以下の条件を付加しても影響ない
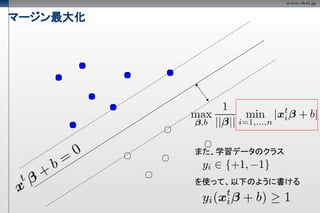
- 26. マージン最大化 また、学習データのクラス を使って、以下のように書ける
- 27. マージン最大化
- 28. マージン最大化 よって、以下のように定式化出来る を解きやすい に置き換えている
- 29. サポートベクターマシン 実データの解析に広く利用されている判別手法 特徴 マージン最大化を基準とすることで、高い判別性能を実 現 カーネル関数を用いた柔軟なモデリング パラメータ推定が凸2次最適化問題として定式化されるた め、高速な最適化アルゴリズムが利用可能
- 30. カーネル関数を用いた柔軟なモデリング この特徴空間上の分布は 、明らかに線形分離可能で はない x2 カーネル関数を使って、元 のデータよりも高い次元の 空間に写像する x1
- 31. 非線形変換 データを高次元の空間へ写す 内積は
- 32. 非線形変換 高次元に写像することで、線形分離可能になる φ3(x) x2 φ1(x) φ2(x) x1
- 33. ハードマージンとソフトマージン 今までの前提 線形分離可能 出来ない場合でも、高次元空間への写像を使うことで線 形分離可能 このように、学習線形分離可能をという条件のマー ジンをハードマージンという
- 34. ハードマージンとソフトマージン 高次元空間への写像でも線形分離可能になるとは 限らない 線形分離可能でない場合、基準を少し緩めたソフト マージンを最大化する 多少の誤識別を許す 特徴2 特徴1
- 35. サポートベクターマシン 実データの解析に広く利用されている判別手法 特徴 マージン最大化を基準とすることで、高い判別性能を実 現 カーネル関数を用いた柔軟なモデリング パラメータ推定が凸2次最適化問題として定式化されるた め、高速な最適化アルゴリズムが利用可能
- 36. パラメータ推定 マージン最大化の学習過程は、ラグランジュ関数を 用いることで、凸2次計画問題になる サンプル数が増えると急激に計算量がふえるため、 分割統治法の考え方を用いた手法が提案されてい る
- 37. パラメータ推定 マージン最大化の学習過程は、ラグランジュ関数を 用いることで、凸2次計画問題になる サンプル数が増えると急激に計算量がふえるため、 分割統治法の考え方を用いた手法が提案されてい る
- 38. 関数をベクトルで考える 1次関数 は、 平面上で、各点 に高さ を 与えると、 空間中の平面を表す
- 39. 勾配 x軸に平行な方向に1だけ進むと関数値は、aだけ増 え、 y軸に平行な方向に距離1だけ進むと 関数値はbだけ増える x軸、y軸方向への勾配の大きさがそれぞれ、a,b。これらを成 分とするベクトルを勾配と呼ぶ 勾配は、関数値がもっとも急激に増大する方向を表す
- 40. 関数の等高線と勾配 xy平面上で関数値が一定の軌跡を等高線と呼ぶ。 点(x, y)での関数値をcとすると、点(x, y)は等高線 上にある。 の勾配は、等高線 と直交す る 勾配は、関数値がもっとも増大する方向 等高線がもっとも増大する方向は垂直方向 等高線 の法線ベクトルは勾配
- 41. n変数関数への拡張 以上のことは、n変数関数でも成り立つ n変数関数の勾配は、次のように定義される n変数関数 の勾配 は、 等値面 の法線ベクトルである
- 42. ラグランジュの未定乗数法 制約条件が1つの場合 制約条件 のもとで関数 が極値を とる点は と置くと、次の式を満たす
- 43. ラグランジュの未定乗数法 制約条件が1つの場合 制約条件 のもとで関数 が極値を とる点は と置くと、次の式を満たす ラグランジュ乗数
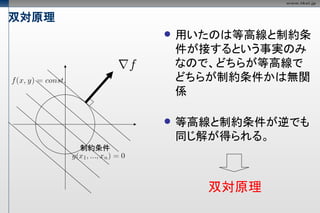
- 44. ラグランジュの未定乗数法 解となる点を通る等高線は 、制約式に接していなけれ ばならない このことは、接点で両者の 法線ベクトルが平行である ことを意味する 制約条件
- 45. 双対原理 用いたのは等高線と制約条 件が接するという事実のみ なので、どちらが等高線で どちらが制約条件かは無関 係 等高線と制約条件が逆でも 同じ解が得られる。 制約条件 双対原理
- 46. ラグランジュ未定乗数法 制約条件が複数の場合 制約条件 のもとで関数 が極値を とる点は と置くと、次の式を満たす
- 47. 線形計画と非線形計画 線形計画 線形制約条件のもとで線形関数を最大、最小にする 問題 シンプレックス法とか使える 非線形計画 非線形制約条件のもとで非線形関数を最大、最小に する問題 一般的な理論も解法も存在しない 制約条件や目的関数のもつ性質ごとに種々の定理が成立 し、さまざまな解法が存在する
- 48. 線形計画と非線形計画 線形計画 線形制約条件のもとで線形関数を最大、最小にする 問題 シンプレックス法とか使える 非線形計画 非線形制約条件のもとで非線形関数を最大、最小に する問題 一般的な理論も解法も存在しない 制約条件や目的関数のもつ性質ごとに種々の定理が成立 し、さまざまな解法が存在する
- 49. 非線形計画とラグランジュ乗数 問題A は上に凸、 は全て下に凸、 は全て1 次式とする
- 50. 非線形計画とラグランジュ乗数 このとき、以下のような関数を考える 上の式を、問題Aのラグランジュ関数と呼ぶ また、このとき、KKT条件が成り立つ 問題Aの解が存在する必要十分条件は、次の条件が成 り立つような が存在すること
- 51. 双対問題 ラグランジュ関数Lにおいて、ラグランジュ乗数 {λi}、{μi}を定数とみなしてxに関して最大化した値 は{λi}、{μi}の関数である。これを と置くと、次の問題を問題Aの双対問題と呼ぶ 問題B
- 52. パラメータ推定の定式化 マージンの最大化
- 53. パラメータ推定の定式化 ラグランジュ乗数αを導入すると、ラグランジュ関数は、
- 54. パラメータ推定の定式化
- 55. パラメータ推定の定式化 よって、相対形式として、以下の凸2次計画問題を解 けばよい これを解く手法として、SMOなどがある
- 56. RによるSVMの使用例
- 57. スパムメールの学習と判別 4601 の電子メールを58 項目に分けて記録したもの 第58 列がクラス情報spam,nonspam で、残りの57 項目はメールの特徴
- 58. ご清聴ありがとうございました。
- 59. 参考文献 わかりやすいパターン認識 データマイニング手法― 営業、マーケティング、カスタマーサポートのための顧客分析 Rによるデータサイエンス - データ解析の基礎から最新手法まで パターン認識 (Rで学ぶデータサイエンス 5) マシンラーニング (Rで学ぶデータサイエンス 6) これなら分かる最適化数学―基礎原理から計算手法まで