Splay Trees

Table of content
Previous
Quiz
Next

Splay trees are the altered versions of the Binary Search Trees, since it contains all the operations of BSTs, like insertion, deletion and searching, followed by another extended operation called splaying.

For instance, a value "A" is supposed to be inserted into the tree. If the tree is empty, add "A" to the root of the tree and exit; but if the tree is not empty, use binary search insertion operation to insert the element and then perform splaying on the new node.

Similarly, after searching an element in the splay tree, the node consisting of the element must be splayed as well.

But how do we perform splaying? Splaying, in simpler terms, is just a process to bring an operational node to the root. There are six types of rotations for it.

  • Zig rotation

  • Zag rotation

  • Zig-Zig rotation

  • Zag-Zag rotation

  • Zig-Zag rotation

  • Zag-Zig rotation

Zig rotation

The zig rotations are performed when the operational node is either the root node or the left child node of the root node. The node is rotated towards its right.

Zig rotation

After the shift, the tree will look like −

after shift

Zag rotation

The zag rotations are also performed when the operational node is either the root node or the right child nod of the root node. The node is rotated towards its left.

Zag rotation

The operational node becomes the root node after the shift −

root node

Zig-Zig rotation

The zig-zig rotations are performed when the operational node has both parent and a grandparent. The node is rotated two places towards its right.

Zig Zig rotation

The first rotation will shift the tree to one position right −

root node 5

The second right rotation will once again shift the node for one position. The final tree after the shift will look like this −

root node 3

Zag-Zag rotation

The zag-zag rotations are also performed when the operational node has both parent and a grandparent. The node is rotated two places towards its left.

Zag Zag rotation

After the first rotation, the tree will look like −

after first rotation

Then the final tree after the second rotation is given as follows. However, the operational node is still not the root so the splaying is considered incomplete. Hence, other suitable rotations are again applied in this case until the node becomes the root.

after second rotatio

Zig-Zag rotation

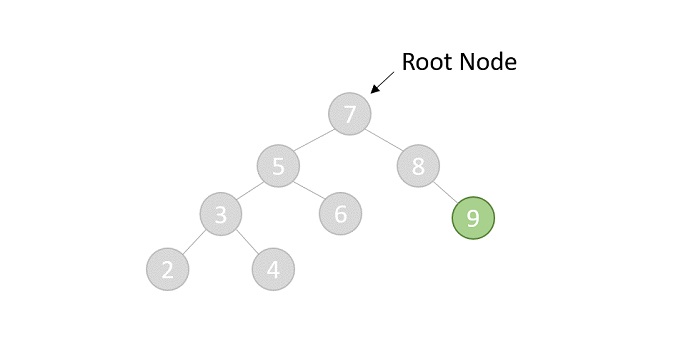
The zig-zag rotations are performed when the operational node has both a parent and a grandparent. But the difference is the grandparent, parent and child are in LRL format. The node is rotated first towards its right followed by left.

Zig Zag rotation

After the first rotation, the tree is −

left rotation

The final tree after the second rotation −

root node 8

Zag-Zig rotation

The zag-zig rotations are also performed when the operational node has both parent and grandparent. But the difference is the grandparent, parent and child are in RLR format. The node is rotated first towards its left followed by right.

Zag Zig rotation

First rotation is performed, the tree is obtained as −

tree obtained

After second rotation, the final tree is given as below. However, the operational node is not the root node yet so one more rotation needs to be performed to make the said node as the root.

after second rotation

Basic Operations of Splay Trees

A splay contains the same basic operations that a Binary Search Tree provides with: Insertion, Deletion, and Search. However, after every operation there is an additional operation that differs them from Binary Search tree operations: Splaying. We have learned about Splaying already so let us understand the procedures of the other operations.

Insertion operation

The insertion operation in a Splay tree is performed in the exact same way insertion in a binary search tree is performed. The procedure to perform the insertion in a splay tree is given as follows −

  • Check whether the tree is empty; if yes, add the new node and exit

insertion

  • If the tree is not empty, add the new node to the existing tree using the binary search insertion.

adding nodes

  • Then, suitable splaying is chosen and applied on the newly added node.

splaying chosen

Zag (Left) Rotation is applied on the new node

left rotation applied

Example

Following are the implementations of this operation in various programming languages −

C C++ Java Python 
#include <stdio.h>
#include <stdlib.h>
struct node {
   int data;
   struct node *leftChild, *rightChild;
};
struct node* newNode(int data){
   struct node* Node = (struct node*)malloc(sizeof(struct node));
   Node->data = data;
   Node->leftChild = Node->rightChild = NULL;
   return (Node);
}
struct node* rightRotate(struct node *x){
   struct node *y = x->leftChild;
   x->leftChild = y->rightChild;
   y->rightChild = x;
   return y;
}
struct node* leftRotate(struct node *x){
   struct node *y = x->rightChild;
   x->rightChild = y->leftChild;
   y->leftChild = x;
   return y;
}
struct node* splay(struct node *root, int data){
   if (root == NULL || root->data == data)
      return root;
   if (root->data > data) {
      if (root->leftChild == NULL) return root;
      if (root->leftChild->data > data) {
         root->leftChild->leftChild = splay(root->leftChild->leftChild, data);
         root = rightRotate(root);
      } else if (root->leftChild->data < data) {
         root->leftChild->rightChild = splay(root->leftChild->rightChild, data);
         if (root->leftChild->rightChild != NULL)
            root->leftChild = leftRotate(root->leftChild);
      }
      return (root->leftChild == NULL)? root: rightRotate(root);
   } else {
      if (root->rightChild == NULL) return root;
      if (root->rightChild->data > data) {
         root->rightChild->leftChild = splay(root->rightChild->leftChild, data);
         if (root->rightChild->leftChild != NULL)
            root->rightChild = rightRotate(root->rightChild);
      } else if (root->rightChild->data < data) {
         root->rightChild->rightChild = splay(root->rightChild->rightChild, data);
         root = leftRotate(root);
      }
      return (root->rightChild == NULL)? root: leftRotate(root);
   }
}
struct node* insert(struct node *root, int k){
   if (root == NULL) return newNode(k);
   root = splay(root, k);
   if (root->data == k) return root;
   struct node *newnode = newNode(k);
   if (root->data > k) {
      newnode->rightChild = root;
      newnode->leftChild = root->leftChild;
      root->leftChild = NULL;
   } else {
      newnode->leftChild = root;
      newnode->rightChild = root->rightChild;
      root->rightChild = NULL;
   }
   return newnode;
}
void printTree(struct node *root){
   if (root == NULL)
      return;
   if (root != NULL) {
      printTree(root->leftChild);
      printf("%d ", root->data);
      printTree(root->rightChild);
   }
}
int main(){
   struct node* root = newNode(34);
   root->leftChild = newNode(15);
   root->rightChild = newNode(40);
   root->leftChild->leftChild = newNode(12);
   root->leftChild->leftChild->rightChild = newNode(14);
   root->rightChild->rightChild = newNode(59);
   printf("The Splay tree is: \n");
   printTree(root);
   return 0;
}

Output

The Splay tree is: 
12 14 15 34 40 59 

#include <iostream>
struct node {
   int data;
   struct node *leftChild, *rightChild;
};
struct node* newNode(int data){
   struct node* Node = (struct node*)malloc(sizeof(struct node));
   Node->data = data;
   Node->leftChild = Node->rightChild = NULL;
   return (Node);
}
struct node* rightRotate(struct node *x){
   struct node *y = x->leftChild;
   x->leftChild = y->rightChild;
   y->rightChild = x;
   return y;
}
struct node* leftRotate(struct node *x){
   struct node *y = x->rightChild;
   x->rightChild = y->leftChild;
   y->leftChild = x;
   return y;
}
struct node* splay(struct node *root, int data){
   if (root == NULL || root->data == data)
      return root;
   if (root->data > data) {
      if (root->leftChild == NULL) return root;
      if (root->leftChild->data > data) {
         root->leftChild->leftChild = splay(root->leftChild->leftChild, data);
         root = rightRotate(root);
      } else if (root->leftChild->data < data) {
         root->leftChild->rightChild = splay(root->leftChild->rightChild, data);
         if (root->leftChild->rightChild != NULL)
            root->leftChild = leftRotate(root->leftChild);
      }
      return (root->leftChild == NULL)? root: rightRotate(root);
   } else {
      if (root->rightChild == NULL) return root;
      if (root->rightChild->data > data) {
         root->rightChild->leftChild = splay(root->rightChild->leftChild, data);
         if (root->rightChild->leftChild != NULL)
            root->rightChild = rightRotate(root->rightChild);
      } else if (root->rightChild->data < data) {
         root->rightChild->rightChild = splay(root->rightChild->rightChild, data);
         root = leftRotate(root);
      }
      return (root->rightChild == NULL)? root: leftRotate(root);
   }
}
struct node* insert(struct node *root, int k){
   if (root == NULL) return newNode(k);
   root = splay(root, k);
   if (root->data == k) return root;
   struct node *newnode = newNode(k);
   if (root->data > k) {
      newnode->rightChild = root;
      newnode->leftChild = root->leftChild;
      root->leftChild = NULL;
   } else {
      newnode->leftChild = root;
      newnode->rightChild = root->rightChild;
      root->rightChild = NULL;
   }
   return newnode;
}
void printTree(struct node *root){
   if (root == NULL)
      return;
   if (root != NULL) {
      printTree(root->leftChild);
      printf("%d ", root->data);
      printTree(root->rightChild);
   }
}
int main(){
   struct node* root = newNode(34);
   root->leftChild = newNode(15);
   root->rightChild = newNode(40);
   root->leftChild->leftChild = newNode(12);
   root->leftChild->leftChild->rightChild = newNode(14);
   root->rightChild->rightChild = newNode(59);
   printf("The Splay tree is: \n");
   printTree(root);
   return 0;
}

Output

The Splay tree is: 
12 14 15 34 40 59 

import java.io.*;
public class SplayTree {
   static class node {
      int data;
      node leftChild, rightChild;
   };
   static node newNode(int data) {
      node Node = new node();
      Node.data = data;
      Node.leftChild = Node.rightChild = null;
      return (Node);
   }
   static node rightRotate(node x) {
      node y = x.leftChild;
      x.leftChild = y.rightChild;
      y.rightChild = x;
      return y;
   }
   static node leftRotate(node x) {
      node y = x.rightChild;
      x.rightChild = y.leftChild;
      y.leftChild = x;
      return y;
   }
   static node splay(node root, int data) {
      if (root == null || root.data == data)
         return root;
      if (root.data > data) {
         if (root.leftChild == null) return root;
         if (root.leftChild.data > data) {
            root.leftChild.leftChild = splay(root.leftChild.leftChild, data);
            root = rightRotate(root);
         } else if (root.leftChild.data < data) {
            root.leftChild.rightChild = splay(root.leftChild.rightChild, data);
            if (root.leftChild.rightChild != null)
               root.leftChild = leftRotate(root.leftChild);
         }
         return (root.leftChild == null)? root: rightRotate(root);
      } else {
         if (root.rightChild == null) return root;
         if (root.rightChild.data > data) {
            root.rightChild.leftChild = splay(root.rightChild.leftChild, data);
            if (root.rightChild.leftChild != null)
               root.rightChild = rightRotate(root.rightChild);
         } else if (root.rightChild.data < data) {
            root.rightChild.rightChild = splay(root.rightChild.rightChild, data);
            root = leftRotate(root);
         }
         return (root.rightChild == null)? root: leftRotate(root);
      }
   }
   static node insert(node root, int k) {
      if (root == null) return newNode(k);
      root = splay(root, k);
      if (root.data == k) return root;
      node newnode = newNode(k);
      if (root.data > k) {
         newnode.rightChild = root;
         newnode.leftChild = root.leftChild;
         root.leftChild = null;
      } else {
         newnode.leftChild = root;
         newnode.rightChild = root.rightChild;
         root.rightChild = null;
      }
      return newnode;
   }
   static void printTree(node root) {
      if (root == null)
         return;
      if (root != null) {
         printTree(root.leftChild);
         System.out.print(root.data + " ");
         printTree(root.rightChild);
      }
   }
   public static void main(String args[]) {
      node root = newNode(34);
      root.leftChild = newNode(15);
      root.rightChild = newNode(40);
      root.leftChild.leftChild = newNode(12);
      root.leftChild.leftChild.rightChild = newNode(14);
      root.rightChild.rightChild = newNode(59);
      System.out.println("The Splay tree is: ");
      printTree(root);
   }
}

Output

The Splay tree is: 
12 14 15 34 40 59 

#Python Code for Insertion Operation of Splay Trees
class Node:
    def __init__(self, data):
        self.data = data
        self.leftChild = None
        self.rightChild = None
def newNode(data):
    return Node(data)
def rightRotate(x):
    y = x.leftChild
    x.leftChild = y.rightChild
    y.rightChild = x
    return y
def leftRotate(x):
    y = x.rightChild
    x.rightChild = y.leftChild
    y.leftChild = x
    return y
def splay(root, data):
    if root is None or root.data == data:
        return root
    if root.data > data:
        if root.leftChild is None:
            return root
        if root.leftChild.data > data:
            root.leftChild.leftChild = splay(root.leftChild.leftChild, data)
            root = rightRotate(root)
        elif root.leftChild.data < data:
            root.leftChild.rightChild = splay(root.leftChild.rightChild, data)
            if root.leftChild.rightChild is not None:
                root.leftChild = leftRotate(root.leftChild)
        return root if root.leftChild is None else rightRotate(root)
    else:
        if root.rightChild is None:
            return root
        if root.rightChild.data > data:
            root.rightChild.leftChild = splay(root.rightChild.leftChild, data)
            if root.rightChild.leftChild is not None:
                root.rightChild = rightRotate(root.rightChild)
        elif root.rightChild.data < data:
            root.rightChild.rightChild = splay(root.rightChild.rightChild, data)
            root = leftRotate(root)
        return root if root.rightChild is None else leftRotate(root)
def insert(root, k):
    if root is None:
        return newNode(k)
    root = splay(root, k)
    if root.data == k:
        return root
    newnode = newNode(k)
    if root.data > k:
        newnode.rightChild = root
        newnode.leftChild = root.leftChild
        root.leftChild = None
    else:
        newnode.leftChild = root
        newnode.rightChild = root.rightChild
        root.rightChild = None
    return newnode
def printTree(root):
    if root is None:
        return
    if root is not None:
        printTree(root.leftChild)
        print(root.data, end=" ")
        printTree(root.rightChild)
if __name__ == "__main__":
    root = newNode(34)
    root.leftChild = newNode(15)
    root.rightChild = newNode(40)
    root.leftChild.leftChild = newNode(12)
    root.leftChild.leftChild.rightChild = newNode(14)
    root.rightChild.rightChild = newNode(59)
    print("The Splay tree is: ")
    printTree(root)

Output

The Splay tree is:
12 14 15 34 40 59

Deletion operation

The deletion operation in a splay tree is performed as following −

  • Apply splaying operation on the node to be deleted.

  • Once, the node is made the root, delete the node.

  • Now, the tree is split into two trees, the left subtree and the right subtree; with their respective first nodes as the root nodes: say root_left and root_right.

delete

  • If root_left is a NULL value, then the root_right will become the root of the tree. And vice versa.

  • But if both root_left and root_right are not NULL values, then select the maximum value from the left subtree and make it the new root by connecting the subtrees.

deleted 5 node

Example

Following are the implementations of Splay Tree deletion operation in various programming languages −

C C++ Java Python 
#include <stdio.h>
#include <stdlib.h>
struct node {
   int data;
   struct node *leftChild, *rightChild;
};
struct node* newNode(int data){
   struct node* Node = (struct node*)malloc(sizeof(struct node));
   Node->data = data;
   Node->leftChild = Node->rightChild = NULL;
   return (Node);
}
struct node* rightRotate(struct node *x){
   struct node *y = x->leftChild;
   x->leftChild = y->rightChild;
   y->rightChild = x;
   return y;
}
struct node* leftRotate(struct node *x){
   struct node *y = x->rightChild;
   x->rightChild = y->leftChild;
   y->leftChild = x;
   return y;
}
struct node* splay(struct node *root, int data){
   if (root == NULL || root->data == data)
      return root;
   if (root->data > data) {
      if (root->leftChild == NULL) return root;
      if (root->leftChild->data > data) {
         root->leftChild->leftChild = splay(root->leftChild->leftChild, data);
         root = rightRotate(root);
      } else if (root->leftChild->data < data) {
         root->leftChild->rightChild = splay(root->leftChild->rightChild, data);
         if (root->leftChild->rightChild != NULL)
            root->leftChild = leftRotate(root->leftChild);
      }
      return (root->leftChild == NULL)? root: rightRotate(root);
   } else {
      if (root->rightChild == NULL) return root;
      if (root->rightChild->data > data) {
         root->rightChild->leftChild = splay(root->rightChild->leftChild, data);
         if (root->rightChild->leftChild != NULL)
            root->rightChild = rightRotate(root->rightChild);
      } else if (root->rightChild->data < data) {
         root->rightChild->rightChild = splay(root->rightChild->rightChild, data);
         root = leftRotate(root);
      }
      return (root->rightChild == NULL)? root: leftRotate(root);
   }
}
struct node* insert(struct node *root, int k){
   if (root == NULL) return newNode(k);
   root = splay(root, k);
   if (root->data == k) return root;
   struct node *newnode = newNode(k);
   if (root->data > k) {
      newnode->rightChild = root;
      newnode->leftChild = root->leftChild;
      root->leftChild = NULL;
   } else {
      newnode->leftChild = root;
      newnode->rightChild = root->rightChild;
      root->rightChild = NULL;
   }
   return newnode;
}
struct node* deletenode(struct node* root, int data){
   struct node* temp;
   if (root == NULL)
      return NULL;
   root = splay(root, data);
   if (data != root->data)
      return root;
   if (!root->leftChild) {
      temp = root;
      root = root->rightChild;
   } else {
      temp = root;
      root = splay(root->leftChild, data);
      root->rightChild = temp->rightChild;
   }
   free(temp);
   return root;
}
void printTree(struct node *root){
   if (root == NULL)
      return;
   if (root != NULL) {
      printTree(root->leftChild);
      printf("%d ", root->data);
      printTree(root->rightChild);
   }
}
int main(){
   struct node* root = newNode(34);
   root->leftChild = newNode(15);
   root->rightChild = newNode(40);
   printf("The Splay tree is \n");
   printTree(root);
   root = deletenode(root, 40);
   printf("\nThe Splay tree after deletion is \n");
   printTree(root);
   return 0;
}

Output

The Splay tree is 
15 34 40 
The Splay tree after deletion is 
15 34 

#include <iostream>
struct node {
   int data;
   struct node *leftChild, *rightChild;
};
struct node* newNode(int data){
   struct node* Node = (struct node*)malloc(sizeof(struct node));
   Node->data = data;
   Node->leftChild = Node->rightChild = NULL;
   return (Node);
}
struct node* rightRotate(struct node *x){
   struct node *y = x->leftChild;
   x->leftChild = y->rightChild;
   y->rightChild = x;
   return y;
}
struct node* leftRotate(struct node *x){
   struct node *y = x->rightChild;
   x->rightChild = y->leftChild;
   y->leftChild = x;
   return y;
}
struct node* splay(struct node *root, int data){
   if (root == NULL || root->data == data)
      return root;
   if (root->data > data) {
      if (root->leftChild == NULL) return root;
      if (root->leftChild->data > data) {
         root->leftChild->leftChild = splay(root->leftChild->leftChild, data);
         root = rightRotate(root);
      } else if (root->leftChild->data < data) {
         root->leftChild->rightChild = splay(root->leftChild->rightChild, data);
         if (root->leftChild->rightChild != NULL)
            root->leftChild = leftRotate(root->leftChild);
      }
      return (root->leftChild == NULL)? root: rightRotate(root);
   } else {
      if (root->rightChild == NULL) return root;
      if (root->rightChild->data > data) {
         root->rightChild->leftChild = splay(root->rightChild->leftChild, data);
         if (root->rightChild->leftChild != NULL)
            root->rightChild = rightRotate(root->rightChild);
      } else if (root->rightChild->data < data) {
         root->rightChild->rightChild = splay(root->rightChild->rightChild, data);
         root = leftRotate(root);
      }
      return (root->rightChild == NULL)? root: leftRotate(root);
   }
}
struct node* insert(struct node *root, int k){
   if (root == NULL) return newNode(k);
   root = splay(root, k);
   if (root->data == k) return root;
   struct node *newnode = newNode(k);
   if (root->data > k) {
      newnode->rightChild = root;
      newnode->leftChild = root->leftChild;
      root->leftChild = NULL;
   } else {
      newnode->leftChild = root;
      newnode->rightChild = root->rightChild;
      root->rightChild = NULL;
   }
   return newnode;
}
struct node* deletenode(struct node* root, int data){
   struct node* temp;
   if (root == NULL)
      return NULL;
   root = splay(root, data);
   if (data != root->data)
      return root;
   if (!root->leftChild) {
      temp = root;
      root = root->rightChild;
   } else {
      temp = root;
      root = splay(root->leftChild, data);
      root->rightChild = temp->rightChild;
   }
   free(temp);
   return root;
}
void printTree(struct node *root){
   if (root == NULL)
      return;
   if (root != NULL) {
      printTree(root->leftChild);
      printf("%d ", root->data);
      printTree(root->rightChild);
   }
}
int main(){
   struct node* root = newNode(34);
   root->leftChild = newNode(15);
   root->rightChild = newNode(40);
   printf("The Splay tree is \n");
   printTree(root);
   root = deletenode(root, 40);
   printf("\nThe Splay tree after deletion is \n");
   printTree(root);
   return 0;
}

Output

The Splay tree is 
15 34 40 
The Splay tree after deletion is 
15 34 

import java.io.*;
public class SplayTree {
   static class node {
      int data;
      node leftChild, rightChild;
   };
   static node newNode(int data) {
      node Node = new node();
      Node.data = data;
      Node.leftChild = Node.rightChild = null;
      return (Node);
   }
   static node rightRotate(node x) {
      node y = x.leftChild;
      x.leftChild = y.rightChild;
      y.rightChild = x;
      return y;
   }
   static node leftRotate(node x) {
      node y = x.rightChild;
      x.rightChild = y.leftChild;
      y.leftChild = x;
      return y;
   }
   static node splay(node root, int data) {
      if (root == null || root.data == data)
         return root;
      if (root.data > data) {
         if (root.leftChild == null) return root;
         if (root.leftChild.data > data) {
            root.leftChild.leftChild = splay(root.leftChild.leftChild, data);
            root = rightRotate(root);
         } else if (root.leftChild.data < data) {
            root.leftChild.rightChild = splay(root.leftChild.rightChild, data);
            if (root.leftChild.rightChild != null)
               root.leftChild = leftRotate(root.leftChild);
         }
         return (root.leftChild == null)? root: rightRotate(root);
      } else {
         if (root.rightChild == null) return root;
         if (root.rightChild.data > data) {
            root.rightChild.leftChild = splay(root.rightChild.leftChild, data);
            if (root.rightChild.leftChild != null)
               root.rightChild = rightRotate(root.rightChild);
         } else if (root.rightChild.data < data) {
            root.rightChild.rightChild = splay(root.rightChild.rightChild, data);
            root = leftRotate(root);
         }
         return (root.rightChild == null)? root: leftRotate(root);
      }
   }
   static node insert(node root, int k) {
      if (root == null) return newNode(k);
      root = splay(root, k);
      if (root.data == k) return root;
      node newnode = newNode(k);
      if (root.data > k) {
         newnode.rightChild = root;
         newnode.leftChild = root.leftChild;
         root.leftChild = null;
      } else {
         newnode.leftChild = root;
         newnode.rightChild = root.rightChild;
         root.rightChild = null;
      }
      return newnode;
   }
   static node deletenode(node root, int data) {
      node temp;
      if (root == null)
         return null;
      root = splay(root, data);
      if (data != root.data)
         return root;
      if (root.leftChild == null) {
         temp = root;
         root = root.rightChild;
      } else {
         temp = root;
         root = splay(root.leftChild, data);
         root.rightChild = temp.rightChild;
      }
      return root;
   }
   static void printTree(node root) {
      if (root == null)
         return;
      if (root != null) {
         printTree(root.leftChild);
         System.out.print(root.data + " ");
         printTree(root.rightChild);
      }
   }
   public static void main(String args[]) {
      node root = newNode(34);
      root.leftChild = newNode(15);
      root.rightChild = newNode(40);
      System.out.println("The Splay tree is: ");
      printTree(root);
      root = deletenode(root, 40);
      System.out.println("\nThe Splay tree after deletion is: ");
      printTree(root);
   }
}

Output

The Splay tree is: 
15 34 40 
The Splay tree after deletion is: 
15 34 

#Python Code for Deletion operation of Splay Trees 
class Node:
    def __init__(self, data):
        self.data = data
        self.leftChild = None
        self.rightChild = None
def newNode(data):
    node = Node(data)
    return node
def rightRotate(x):
    y = x.leftChild
    x.leftChild = y.rightChild
    y.rightChild = x
    return y
def leftRotate(x):
    y = x.rightChild
    x.rightChild = y.leftChild
    y.leftChild = x
    return y
def splay(root, data):
    if root is None or root.data == data:
        return root
    if root.data > data:
        if root.leftChild is None:
            return root 
        if root.leftChild.data > data:
            root.leftChild.leftChild = splay(root.leftChild.leftChild, data)
            root = rightRotate(root)
        elif root.leftChild.data < data:
            root.leftChild.rightChild = splay(root.leftChild.rightChild, data)
            if root.leftChild.rightChild is not None:
                root.leftChild = leftRotate(root.leftChild)
        return root if root.leftChild is None else rightRotate(root)
    else:
        if root.rightChild is None:
            return root
        if root.rightChild.data > data:
            root.rightChild.leftChild = splay(root.rightChild.leftChild, data)
            if root.rightChild.leftChild is not None:
                root.rightChild = rightRotate(root.rightChild)
        elif root.rightChild.data < data:
            root.rightChild.rightChild = splay(root.rightChild.rightChild, data)
            root = leftRotate(root)
        return root if root.rightChild is None else leftRotate(root)
def insert(root, k):
    if root is None:
        return newNode(k)
    root = splay(root, k)
    if root.data == k:
        return root  
    newnode = newNode(k)
    if root.data > k:
        newnode.rightChild = root
        newnode.leftChild = root.leftChild
        root.leftChild = None
    else:
        newnode.leftChild = root
        newnode.rightChild = root.rightChild
        root.rightChild = None 
    return newnode
def deletenode(root, data):
    temp = None
    if root is None:
        return None
    root = splay(root, data)
    if data != root.data:
        return root
    if root.leftChild is None:
        temp = root
        root = root.rightChild
    else:
        temp = root
        root = splay(root.leftChild, data)
        root.rightChild = temp.rightChild
    del temp
    return root
def printTree(root):
    if root is None:
        return
    if root is not None:
        printTree(root.leftChild)
        print(root.data, end=" ")
        printTree(root.rightChild)
root = newNode(34)
root.leftChild = newNode(15)
root.rightChild = newNode(40)
print("The Splay tree is:")
printTree(root)
root = deletenode(root, 40)
print("\nThe Splay tree after deletion is:")
printTree(root)

Output

The Splay tree is:
15 34 40 
The Splay tree after deletion is:
15 34

The search operation in a Splay tree follows the same procedure of the Binary Search Tree operation. However, after the searching is done and the element is found, splaying is applied on the node searched. If the element is not found, then unsuccessful search is prompted.

Example

Following are the implementations of this operation in various programming languages −

C C++ Java Python 
#include <stdio.h>
#include <stdlib.h>
struct node {
   int data;
   struct node *leftChild, *rightChild;
};
struct node* newNode(int data){
   struct node* Node = (struct node*)malloc(sizeof(struct node));
   Node->data = data;
   Node->leftChild = Node->rightChild = NULL;
   return (Node);
}
struct node* rightRotate(struct node *x){
   struct node *y = x->leftChild;
   x->leftChild = y->rightChild;
   y->rightChild = x;
   return y;
}
struct node* leftRotate(struct node *x){
   struct node *y = x->rightChild;
   x->rightChild = y->leftChild;
   y->leftChild = x;
   return y;
}
struct node* splay(struct node *root, int data){
   if (root == NULL || root->data == data)
      return root;
   if (root->data > data) {
      if (root->leftChild == NULL) return root;
      if (root->leftChild->data > data) {
         root->leftChild->leftChild = splay(root->leftChild->leftChild, data);
         root = rightRotate(root);
      } else if (root->leftChild->data < data) {
         root->leftChild->rightChild = splay(root->leftChild->rightChild, data);
         if (root->leftChild->rightChild != NULL)
            root->leftChild = leftRotate(root->leftChild);
      }
      return (root->leftChild == NULL)? root: rightRotate(root);
   } else {
      if (root->rightChild == NULL) return root;
      if (root->rightChild->data > data) {
         root->rightChild->leftChild = splay(root->rightChild->leftChild, data);
         if (root->rightChild->leftChild != NULL)
            root->rightChild = rightRotate(root->rightChild);
      } else if (root->rightChild->data < data) {
         root->rightChild->rightChild = splay(root->rightChild->rightChild, data);
         root = leftRotate(root);
      }
      return (root->rightChild == NULL)? root: leftRotate(root);
   }
}
struct node* insert(struct node *root, int k){
   if (root == NULL) return newNode(k);
   root = splay(root, k);
   if (root->data == k) return root;
   struct node *newnode = newNode(k);
   if (root->data > k) {
      newnode->rightChild = root;
      newnode->leftChild = root->leftChild;
      root->leftChild = NULL;
   } else {
      newnode->leftChild = root;
      newnode->rightChild = root->rightChild;
      root->rightChild = NULL;
   }
   return newnode;
}
struct node* search(struct node* root, int data){
    return splay(root, data);
}
void printTree(struct node *root){
   if (root == NULL)
      return;
   if (root != NULL) {
      printTree(root->leftChild);
      printf("%d ", root->data);
      printTree(root->rightChild);
   }
}
void preOrder(struct node *root) 
{ 
	if (root != NULL) 
	{ 
		printf("%d ", root->data); 
		preOrder(root->leftChild); 
		preOrder(root->rightChild); 
	} 
}
int main(){
   struct node* root = newNode(34);
   root->leftChild = newNode(15);
   root->rightChild = newNode(40);
   root->leftChild->leftChild = newNode(12);
   root->leftChild->leftChild->rightChild = newNode(14);
   root->rightChild->rightChild = newNode(59);
   printf("The Splay tree is \n");
   printTree(root);
   int ele = 14;
   printf("\nElement to be searched: %d", ele);
   root = search(root, ele);
   printf("\nModified preorder traversal if element is found: ");
   preOrder(root);
}

Output

The Splay tree is 
12 14 15 34 40 59 
Element to be searched: 14
Modified preorder traversal if element is found: 14 12 15 34 40 59 

#include <bits/stdc++.h>
using namespace std;
class node{
public:
   int data;
   node *leftChild, *rightChild;
};
node* newNode(int data){
   node* Node = new node();
   Node->data = data;
   Node->leftChild = Node->rightChild = NULL;
   return (Node);
}
node *rightRotate(node *x){
   node *y = x->leftChild;
   x->leftChild = y->rightChild;
   y->rightChild = x;
   return y;
}
node *leftRotate(node *x){
   node *y = x->rightChild;
   x->rightChild = y->leftChild;
   y->leftChild = x;
   return y;
}
node *splay(node *root, int data){
   if (root == NULL || root->data == data)
      return root;
   if (root->data > data) {
      if (root->leftChild == NULL) return root;
      if (root->leftChild->data > data) {
         root->leftChild->leftChild = splay(root->leftChild->leftChild, data);
         root = rightRotate(root);
      } else if (root->leftChild->data < data) {
         root->leftChild->rightChild = splay(root->leftChild->rightChild, data);
         if (root->leftChild->rightChild != NULL)
            root->leftChild = leftRotate(root->leftChild);
      }
      return (root->leftChild == NULL)? root: rightRotate(root);
   } else {
      if (root->rightChild == NULL) return root;
      if (root->rightChild->data > data) {
         root->rightChild->leftChild = splay(root->rightChild->leftChild, data);
         if (root->rightChild->leftChild != NULL)
            root->rightChild = rightRotate(root->rightChild);
      } else if (root->rightChild->data < data) {
         root->rightChild->rightChild = splay(root->rightChild->rightChild, data);
         root = leftRotate(root);
      }
      return (root->rightChild == NULL)? root: leftRotate(root);
   }
}
node* insert(node *root, int k)
{
   if (root == NULL) return newNode(k);
   root = splay(root, k);
   if (root->data == k) return root;
   node *newnode = newNode(k);
   if (root->data > k) {
      newnode->rightChild = root;
      newnode->leftChild = root->leftChild;
      root->leftChild = NULL;
   } else {
      newnode->leftChild = root;
      newnode->rightChild = root->rightChild;
      root->rightChild = NULL;
   }
   return newnode;
}
node* search(struct node* root, int data){
    return splay(root, data);
}
void printTree(node *root){
   if (root == NULL)
      return;
   if (root != NULL) {
      printTree(root->leftChild);
      cout << root->data << " ";
      printTree(root->rightChild);
   }
}
void preOrder(struct node *root) 
{ 
	if (root != NULL) 
	{ 
		cout << root->data << " "; 
		preOrder(root->leftChild); 
		preOrder(root->rightChild); 
	} 
}
int main(){
   node* root = newNode(34);
   root->leftChild = newNode(15);
   root->rightChild = newNode(40);
   root->leftChild->leftChild = newNode(12);
   root->leftChild->leftChild->rightChild = newNode(14);
   root->rightChild->rightChild = newNode(59);
   cout << "The Splay tree is \n";
   printTree(root);
   int ele = 40;
   cout << "\nThe element to be searched: " << ele;
   root = search(root, ele);
   cout << "\nModified preorder traversal if element is found: ";
   preOrder(root);
}

Output

The Splay tree is 
12 14 15 34 40 59 
The element to be searched: 40
Modified preorder traversal if element is found: 40 34 15 12 14 59 

import java.io.*;
public class SplayTree {
   static class node {
      int data;
      node leftChild, rightChild;
   };
   static node newNode(int data) {
      node Node = new node();
      Node.data = data;
      Node.leftChild = Node.rightChild = null;
      return (Node);
   }
   static node rightRotate(node x) {
      node y = x.leftChild;
      x.leftChild = y.rightChild;
      y.rightChild = x;
      return y;
   }
   static node leftRotate(node x) {
      node y = x.rightChild;
      x.rightChild = y.leftChild;
      y.leftChild = x;
      return y;
   }
   static node splay(node root, int data) {
      if (root == null || root.data == data)
         return root;
      if (root.data > data) {
         if (root.leftChild == null) return root;
         if (root.leftChild.data > data) {
            root.leftChild.leftChild = splay(root.leftChild.leftChild, data);
            root = rightRotate(root);
         } else if (root.leftChild.data < data) {
            root.leftChild.rightChild = splay(root.leftChild.rightChild, data);
            if (root.leftChild.rightChild != null)
               root.leftChild = leftRotate(root.leftChild);
         }
         return (root.leftChild == null)? root: rightRotate(root);
      } else {
         if (root.rightChild == null) return root;
         if (root.rightChild.data > data) {
            root.rightChild.leftChild = splay(root.rightChild.leftChild, data);
            if (root.rightChild.leftChild != null)
               root.rightChild = rightRotate(root.rightChild);
         } else if (root.rightChild.data < data) {
            root.rightChild.rightChild = splay(root.rightChild.rightChild, data);
            root = leftRotate(root);
         }
         return (root.rightChild == null)? root: leftRotate(root);
      }
   }
   static node insert(node root, int k) {
      if (root == null) return newNode(k);
      root = splay(root, k);
      if (root.data == k) return root;
      node newnode = newNode(k);
      if (root.data > k) {
         newnode.rightChild = root;
         newnode.leftChild = root.leftChild;
         root.leftChild = null;
      } else {
         newnode.leftChild = root;
         newnode.rightChild = root.rightChild;
         root.rightChild = null;
      }
      return newnode;
   }
   static node search(node root, int key){
       return splay(root, key);
   }
   static void printTree(node root) {
      if (root == null)
         return;
      if (root != null) {
         printTree(root.leftChild);
         System.out.print(root.data + " ");
         printTree(root.rightChild);
      }
   }
   static void preOrder(node root) { 
      if (root != null) { 
	     System.out.print(root.data + " "); 
		 preOrder(root.leftChild); 
		 preOrder(root.rightChild); 
	  } 
   }
   public static void main(String args[]) {
      node root = newNode(34);
      root.leftChild = newNode(15);
      root.rightChild = newNode(40);
      root.leftChild.leftChild = newNode(12);
      root.leftChild.leftChild.rightChild = newNode(14);
      root.rightChild.rightChild = newNode(59);
      System.out.println("The Splay tree is: ");
      printTree(root);
      int ele = 34;
      System.out.print("\nElement to be searched: " + ele);
      root = search(root, ele);
      System.out.print("\nModified preorder traversal if element is found: ");
      preOrder(root);
   }
}

Output

The Splay tree is: 
12 14 15 34 40 59 
Element to be searched: 34
Modified preorder traversal if element is found: 34 15 12 14 40 59

#Python Code for Search Operation of splay Trees
class Node:
    def __init__(self, data):
        self.data = data
        self.leftChild = None
        self.rightChild = None
def newNode(data):
    newNode = Node(data)
    newNode.leftChild = newNode.rightChild = None
    return newNode
def rightRotate(x):
    y = x.leftChild
    x.leftChild = y.rightChild
    y.rightChild = x
    return y
def leftRotate(x):
    y = x.rightChild
    x.rightChild = y.leftChild
    y.leftChild = x
    return y
def splay(root, data):
    if root is None or root.data == data:
        return root
    if root.data > data:
        if root.leftChild is None:
            return root
        if root.leftChild.data > data:
            root.leftChild.leftChild = splay(root.leftChild.leftChild, data)
            root = rightRotate(root)
        elif root.leftChild.data < data:
            root.leftChild.rightChild = splay(root.leftChild.rightChild, data)
            if root.leftChild.rightChild is not None:
                root.leftChild = leftRotate(root.leftChild)   
        return root if root.leftChild is None else rightRotate(root)
    else:
        if root.rightChild is None:
            return root
        if root.rightChild.data > data:
            root.rightChild.leftChild = splay(root.rightChild.leftChild, data)
            if root.rightChild.leftChild is not None:
                root.rightChild = rightRotate(root.rightChild)
        elif root.rightChild.data < data:
            root.rightChild.rightChild = splay(root.rightChild.rightChild, data)
            root = leftRotate(root)
        return root if root.rightChild is None else leftRotate(root)
def insert(root, k):
    if root is None:
        return newNode(k) 
    root = splay(root, k)
    if root.data == k:
        return root
    newnode = newNode(k)
    if root.data > k:
        newnode.rightChild = root
        newnode.leftChild = root.leftChild
        root.leftChild = None
    else:
        newnode.leftChild = root
        newnode.rightChild = root.rightChild
        root.rightChild = None
    return newnode
def search(root, data):
    return splay(root, data)
def printTree(root):
    if root is None:
        return 
    if root is not None:
        printTree(root.leftChild)
        print(root.data, end=" ")
        printTree(root.rightChild)
def preOrder(root):
    if root != None:
        print(root.data, end = " ")
        preOrder(root.leftChild)
        preOrder(root.rightChild)
root = newNode(34)
root.leftChild = newNode(15)
root.rightChild = newNode(40)
root.leftChild.leftChild = newNode(12)
root.leftChild.leftChild.rightChild = newNode(14)
root.rightChild.rightChild = newNode(59)
print("The Splay tree is")
printTree(root)
ele = 59
print("\nElement to be searched ",ele)
root = search(root, ele)
print("Modified preorder traversal if element is found: ")
preOrder(root)

Output

The Splay tree is
12 14 15 34 40 59 
Element to be searched  59
Modified preorder traversal if element is found: 
59 40 34 15 12 14
Print Page
Previous
Next
Advertisements