気に入った記事をブックマーク
- 気に入った記事を保存できます
保存した記事の一覧は、はてなブックマークで確認・編集ができます
- 記事を読んだ感想やメモを書き残せます
- 非公開でブックマークすることもできます
エントリーの編集
エントリーの編集は全ユーザーに共通の機能です。
必ずガイドラインを一読の上ご利用ください。
記事へのコメント90件
- 注目コメント
- 新着コメント
kako-jun
π/180でなく2π/360と覚えよう、が目的なら中途半端だと思う。これだと、なぜ360°を2πにしたの？を説明できない。cos360°が1だからだ。複素数平面上の単位円の円周上を、右端から左回りに1周するイメージで覚えよう
asrog
「ここに半径1の円があるやろ、角度があるやろ、角度で円を切り取って円周ベロンと剥がすやろ、この長さをラジアンっちゅうんや。円の弧の長さで角度書くから弧度法っちゅうねん」が分かってればその先はどうでも。
ene0kcal
そんなところで躓いたことなかったので何言ってるのか最初わからなかったが、わかった。なんで私が躓かなかったのか、π/180をかけるなんて覚えてなくて、2π/360をかけていたからだった。
evans7
最後まで読んだけど便宜上その運用で全く支障がないし、素早さと正確さが求められるスタンダードな試験でしか弧度法を使わない99％の日本人にとってはこの記事は無駄だと思う。（残り1％は数学オタク）
stracciatella
昔フレミングの法則で手を出すのがかっこ悪いという青臭い理由で、脳内右ねじの法則だけで高校物理（電磁気）をやり過ごした。しかし結果的にその方が失敗が無かった。この主張の趣旨はわかる。
注目コメント算出アルゴリズムの一部にLINEヤフー株式会社の「建設的コメント順位付けモデルAPI」を使用しています
いまの話題をアプリでチェック！
- バナー広告なし
- ミュート機能あり
- ダークモード搭載
関連記事
ラジアンへの変換を「π/180をかける」と覚えるのはやめなさい！ - アジマティクス
神様。この記事にうさんくさ自己啓発本みたいなタイトルをつけることをお許しください。 数学のつまずき... 神様。この記事にうさんくさ自己啓発本みたいなタイトルをつけることをお許しください。 数学のつまずきポイントは人それぞれいろいろあると思いますが、高校で出てくる「ラジアン」や「弧度法」とかいうやつが鬼門だったという人、少なくないのではないかと思います。 かいつまんで説明しましょう。我々は角度を表記するのに「度」という単位を使った「度数法」で表記することが多いですが、「度」の代わりに「ラジアン」という単位を使ったものが「弧度法」です。 例えば、度数法でいう「135°」は弧度法では「ラジアン」、「72°」は「ラジアン」となります。 それだけ聞くと、知らない人や忘れてる人からすればなにそれ、ってなるのは当然だと思います。 かくいう私も、いままで平然と「ナニナニ度」と呼んできたものがいきなり「うんちゃらパイ」などと呼ぶようになって、ラジアンを習った当時は面食らったものです。 当時は根本的な理解をして
ブックマークしたユーザー
すべてのユーザーの
詳細を表示します
詳細を表示します
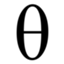
2021/03/15 リンク