Pengguna:Klasüo/bak pasir/khusus/2

"Bilangan Euler" beralih ke halaman ini. Untuk kegunaan lain, lihat Daftar benda yang dinamai menurut nama Leonhard Euler § Bilangan.

"E (bilangan)" beralih ke halaman ini. Untuk kode yang mewakili bahan tambahan makanan, lihat Bilangan E.

Grafik persamaan $y=1/x$. Di antaranya, $e$ adalah bilangan unik yang lebih besar dari 1 yang membuat daerah yang diarsir sama dengan 1.

Bilangan $e$ (atau, disebut juga sebagai bilangan Euler) adalah konstanta matematika yang dimana nilai kira-kiranya sama dengan 2,71828 dan dikarakterisasi dalam berbagai cara. Hal ini termasuk basis dari logaritma alami. Ini adalah limit dari $(1+1/n)^{n}$ sebagai $n$ yang mendekati nilai tak hingga, ekspresi yang muncul dalam studi bunga majemuk. Ini dihitung sebagai jumlah dari deret tak hingga

$e=\sum \limits _{n=0}^{\infty }{\frac {1}{n!}}=1+{\frac {1}{1}}+{\frac {1}{1\cdot 2}}+{\frac {1}{1\cdot 2\cdot 3}}+\cdots$

Ini juga merupakan bilangan positif unik $a$ sehingga grafik fungsi $y=a^{x}$ memiliki kemiringan dari 1 pada $x=0$.

Fungsi eksponensial (alami) $f(x)=e^{x}$ adalah fungsi unik $f$ sama dengan turunan-diri dan memenuhi persamaan $f''(0)=1$; maka seseorang juga mendefinisikan $e$ sebagai $f(1)$. Logaritma alami atau logaritma ke basis $e$, adalah fungsi invers pada fungsi eksponensial alami. Logaritma alamai suatu bilangan $k>1$ didefinisikan secara langsung sebagai luas bawah kurva $y=1/x$ antara $x=1$ dan $x=k$, dalam hal ini $e$ adalah nilai $k$ yang luasnya sama dengan satu (lihat gambar diatas).

$e$ kadang-kadang disebut bilangan Euler, setelah metematikawan asal Swiss Leonhard Euler (jangan keliru dengan $\gamma$, konstanta Euler–Mascheroni, terkadang disebut juga sebagai konstanta Euler), atau konstanta Napier. Namun, pilihan Euler atas simbol $e$ dikatakan sudah dipertahankan untuk menghormatinya. Konstanta ini ditemukan oleh matematikawan Swiss Jacob Bernoulli saat mempelajari bunga majemuk.

Bilangan $e$ sangat penting digunakan dalam bidang matematika, disamping 0, 1, $\pi$, dan $\mathrm {i}$. Kelimanya muncul dalam satu formulasi identitas Euler, dan memainkan peran penting dan berulang di seluruh bidang matematika. Seperti konstanta $\pi$, $e$ adalah irasional (yaitu, tidak dapat direpresentasikan sebagai rasio bilangan bulat) dan transendental (yaitu bukan akar dari polinomial bukan nol dengan koefisien rasional). Untuk 50 tempat desimal nilai $e$ adalah:

2.71828182845904523536028747135266249775724709369995... (barisan A001113 pada OEIS).

Sejarah

Referensi pertama untuk konstanta diterbitkan pada tahun 1618 dalam tabel lampiran dari karya tentang logaritma oleh John Napier. Namun, ini tidak berisi konstanta itu sendiri, tetapi hanya daftar logaritma yang dihitung dari konstanta. Diasumsikan bahwa tabel tersebut ditulis oleh William Oughtred.

Penemuan konstanta itu sendiri dikreditkan ke Jacob Bernoulli pada tahun 1683, yang mencoba mencari nilai dari ekspresi berikut (yang sama dengan $e$):

$\lim _{n\to \infty }\left(1+{\frac {1}{n}}\right)^{n}.$

Penggunaan konstanta yang diketahui pertama kali, diawali oleh huruf $b$ adalah dalam korespondensi dari Gottfried Leibniz hingga Christiaan Huygens pada tahun 1690 dan 1691. Leonhard Euler memperkenalkan huruf $e$ sebagai dasar untuk logaritma alami, ditulis dalam surat kepada Christian Goldbach pada tanggal 25 November 1731. Euler mulai menggunakan huruf $e$ untuk konstanta pada tahun 1727 atau 1728, dalam sebuah makalah yang tidak diterbitkan tentang kekuatan ledakan dalam meriam, sedangkan perkenalan pertama $e$ dalam sebuah publikasi adalah Mechanica Euler (1736). Meskipun beberapa peneliti menggunakan huruf $c$ pada tahun-tahun berikutnya, huruf $e$ lebih umum dan akhirnya menjadi standar.

Dalam matematika, standarnya adalah mengeset konstanta sebagai "$e$" ditulis dalam huruf miring; ISO 80000-2:2019 standar merekomendasikan konstanta pengaturan huruf dalam gaya tegak, tetapi ini belum divalidasikan oleh komunitas ilmiah.

Applications

Compound interest

The effect of earning 20% annual interest on an initial $1,000 investment at various compounding frequencies

Jacob Bernoulli discovered this constant in 1683, while studying a question about compound interest:

An account starts with $1.00 and pays 100 percent interest per year. If the interest is credited once, at the end of the year, the value of the account at year-end will be $2.00. What happens if the interest is computed and credited more frequently during the year?

If the interest is credited twice in the year, the interest rate for each 6 months will be 50%, so the initial $1 is multiplied by 1.5 twice, yielding $1.00 × 1.5² = $2.25 at the end of the year. Compounding quarterly yields $1.00 × 1.25⁴ = $2.4414..., and compounding monthly yields $1.00 × (1 + 1/12)¹² = $2.613035… If there are n compounding intervals, the interest for each interval will be 100%/n and the value at the end of the year will be $1.00 × (1 + 1/n)ⁿ.

Bernoulli noticed that this sequence approaches a limit (the force of interest) with larger n and, thus, smaller compounding intervals. Compounding weekly (n = 52) yields $2.692597..., while compounding daily (n = 365) yields $2.714567... (approximately two cents more). The limit as n grows large is the number that came to be known as e. That is, with continuous compounding, the account value will reach $2.718281828...

More generally, an account that starts at $1 and offers an annual interest rate of R will, after t years, yield e^Rt dollars with continuous compounding.

(Note here that R is the decimal equivalent of the rate of interest expressed as a percentage, so for 5% interest, R = 5/100 = 0.05.)

Bernoulli trials

Graphs of probability P of not observing independent events each of probability 1/n after n Bernoulli trials, and 1 − P  vs n ; it can be observed that as n increases, the probability of a 1/n-chance event never appearing after n tries rapidly converges to 1/e.

The number e itself also has applications in probability theory, in a way that is not obviously related to exponential growth. Suppose that a gambler plays a slot machine that pays out with a probability of one in n and plays it n times. Then, for large n, the probability that the gambler will lose every bet is approximately 1/e. For n = 20, this is already approximately 1/2.79.

This is an example of a Bernoulli trial process. Each time the gambler plays the slots, there is a one in n chance of winning. Playing n times is modeled by the binomial distribution, which is closely related to the binomial theorem and Pascal's triangle. The probability of winning k times out of n trials is:

${\binom {n}{k}}\left({\frac {1}{n}}\right)^{k}\left(1-{\frac {1}{n}}\right)^{n-k}.$

In particular, the probability of winning zero times (k = 0) is

$\left(1-{\frac {1}{n}}\right)^{n}.$

The limit of the above expression, as n tends to infinity, is precisely 1/e.

Standard normal distribution

Artikel utama: Normal distribution

The normal distribution with zero mean and unit standard deviation is known as the standard normal distribution, given by the probability density function

$\phi (x)={\frac {1}{\sqrt {2\pi }}}e^{-{\frac {1}{2}}x^{2}}.$

The constraint of unit variance (and thus also unit standard deviation) results in the 12 in the exponent, and the constraint of unit total area under the curve $\phi (x)$ results in the factor $\textstyle 1/{\sqrt {2\pi }}$.^[proof] This function is symmetric around x = 0, where it attains its maximum value $\textstyle 1/{\sqrt {2\pi }}$, and has inflection points at x = ±1.

Derangements

Artikel utama: Derangement

Another application of e, also discovered in part by Jacob Bernoulli along with Pierre Remond de Montmort, is in the problem of derangements, also known as the hat check problem: n guests are invited to a party, and at the door, the guests all check their hats with the butler, who in turn places the hats into n boxes, each labelled with the name of one guest. But the butler has not asked the identities of the guests, and so he puts the hats into boxes selected at random. The problem of de Montmort is to find the probability that none of the hats gets put into the right box. This probability, denoted by $p_{n}\!$, is:

$p_{n}=1-{\frac {1}{1!}}+{\frac {1}{2!}}-{\frac {1}{3!}}+\cdots +{\frac {(-1)^{n}}{n!}}=\sum _{k=0}^{n}{\frac {(-1)^{k}}{k!}}.$

As the number n of guests tends to infinity, p_n approaches 1/e. Furthermore, the number of ways the hats can be placed into the boxes so that none of the hats are in the right box is n!/e (rounded to the nearest integer for every positive n).

Optimal planning problems

A stick of length L is broken into n equal parts. The value of n that maximizes the product of the lengths is then either

$n=\left\lfloor {\frac {L}{e}}\right\rfloor$ or $\left\lfloor {\frac {L}{e}}\right\rfloor +1.$

The stated result follows because the maximum value of $x^{-1}\ln x$ occurs at $x=e$ (Steiner's problem, discussed below). The quantity $x^{-1}\ln x$ is a measure of information gleaned from an event occurring with probability $1/x$, so that essentially the same optimal division appears in optimal planning problems like the secretary problem.

Asymptotics

The number e occurs naturally in connection with many problems involving asymptotics. An example is Stirling's formula for the asymptotics of the factorial function, in which both the numbers e and π appear:

$n!\sim {\sqrt {2\pi n}}\left({\frac {n}{e}}\right)^{n}.$

As a consequence,

$e=\lim _{n\to \infty }{\frac {n}{\sqrt[{n}]{n!}}}.$

In calculus

The graphs of the functions x ↦ a^x are shown for a = 2 (dotted), a = e (blue), and a = 4 (dashed). They all pass through the point (0,1), but the red line (which has slope 1) is tangent to only e^x there.

The value of the natural log function for argument e, i.e. ln e, equals 1.

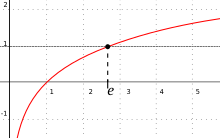
The principal motivation for introducing the number e, particularly in calculus, is to perform differential and integral calculus with exponential functions and logarithms. A general exponential function y = a^x has a derivative, given by a limit:

${\begin{aligned}{\frac {d}{dx}}a^{x}&=\lim _{h\to 0}{\frac {a^{x+h}-a^{x}}{h}}=\lim _{h\to 0}{\frac {a^{x}a^{h}-a^{x}}{h}}\\&=a^{x}\cdot \left(\lim _{h\to 0}{\frac {a^{h}-1}{h}}\right).\end{aligned}}$

The parenthesized limit on the right is independent of the variable x. Its value turns out to be the logarithm of a to base e. Thus, when the value of a is set to e, this limit is equal to 1, and so one arrives at the following simple identity:

${\frac {d}{dx}}e^{x}=e^{x}.$

Consequently, the exponential function with base e is particularly suited to doing calculus. Choosing e (as opposed to some other number as the base of the exponential function) makes calculations involving the derivatives much simpler.

Another motivation comes from considering the derivative of the base-a logarithm (i.e., log_a x), for x > 0:

${\begin{aligned}{\frac {d}{dx}}\log _{a}x&=\lim _{h\to 0}{\frac {\log _{a}(x+h)-\log _{a}(x)}{h}}\\&=\lim _{h\to 0}{\frac {\log _{a}(1+h/x)}{x\cdot h/x}}\\&={\frac {1}{x}}\log _{a}\left(\lim _{u\to 0}(1+u)^{\frac {1}{u}}\right)\\&={\frac {1}{x}}\log _{a}e,\end{aligned}}$

where the substitution u = h/x was made. The base-a logarithm of e is 1, if a equals e. So symbolically,

${\frac {d}{dx}}\log _{e}x={\frac {1}{x}}.$

The logarithm with this special base is called the natural logarithm, and is denoted as ln; it behaves well under differentiation since there is no undetermined limit to carry through the calculations.

Thus, there are two ways of selecting such special numbers a. One way is to set the derivative of the exponential function a^x equal to a^x, and solve for a. The other way is to set the derivative of the base a logarithm to 1/x and solve for a. In each case, one arrives at a convenient choice of base for doing calculus. It turns out that these two solutions for a are actually the same: the number e.

Alternative characterizations

The five colored regions are of equal area, and define units of hyperbolic angle along the hyperbola $xy=1.$

Lihat pula: § Representations, dan Characterizations of the exponential function

Other characterizations of e are also possible: one is as the limit of a sequence, another is as the sum of an infinite series, and still others rely on integral calculus. So far, the following two (equivalent) properties have been introduced:

1. The number e is the unique positive real number such that ${\frac {d}{dt}}e^{t}=e^{t}$.
2. The number e is the unique positive real number such that ${\frac {d}{dt}}\log _{e}t={\frac {1}{t}}$.

The following four characterizations can be proven to be equivalent:

3. The number e is the limit

   $e=\lim _{n\to \infty }\left(1+{\frac {1}{n}}\right)^{n}$

   Similarly:

   $e=\lim _{t\to 0}\left(1+t\right)^{\frac {1}{t}}$

4. The number e is the sum of the infinite series
   $e=\sum _{n=0}^{\infty }{\frac {1}{n!}}={\frac {1}{0!}}+{\frac {1}{1!}}+{\frac {1}{2!}}+{\frac {1}{3!}}+{\frac {1}{4!}}+\cdots ,$
   where n! is the factorial of n.
5. The number e is the unique positive real number such that

   $\int _{1}^{e}{\frac {1}{t}}\,dt=1.$

6. If f(t) is an exponential function, then the quantity $\tau =f(t)/f'(t)$ is a constant, sometimes called the time constant (it is the reciprocal of the exponential growth constant or decay constant). The time constant is the time it takes for the exponential function to increase by a factor of e: $f(t+\tau )=ef(t)$.

Properties

Calculus

As in the motivation, the exponential function e^x is important in part because it is the unique nontrivial function that is its own derivative (up to multiplication by a constant):

${\frac {d}{dx}}e^{x}=e^{x}$

and therefore its own antiderivative as well:

$\int e^{x}\,dx=e^{x}+C.$

Inequalities

Exponential functions y = 2^x and y = 4^x intersect the graph of y = x + 1, respectively, at x = 1 and x = -1/2. The number e is the unique base such that y = e^x intersects only at x = 0. We may infer that e lies between 2 and 4.

The number e is the unique real number such that

$\left(1+{\frac {1}{x}}\right)^{x}<e<\left(1+{\frac {1}{x}}\right)^{x+1}$

for all positive x.

Also, we have the inequality

$e^{x}\geq x+1$

for all real x, with equality if and only if x = 0. Furthermore, e is the unique base of the exponential for which the inequality a^x ≥ x + 1 holds for all x. This is a limiting case of Bernoulli's inequality.

Exponential-like functions

The global maximum of √x occurs at x = e.

Steiner's problem asks to find the global maximum for the function

$f(x)=x^{\frac {1}{x}}.$

This maximum occurs precisely at x = e.

The value of this maximum is 1.4446 6786 1009 7661 3365... (accurate to 20 decimal places).

For proof, the inequality $e^{y}\geq y+1$, from above, evaluated at $y=(x-e)/e$ and simplifying gives $e^{x/e}\geq x$. So $e^{1/e}\geq x^{1/x}$ for all positive x.

Similarly, x = 1/e is where the global minimum occurs for the function

$f(x)=x^{x}$

defined for positive x. More generally, for the function

$f(x)=x^{x^{n}}$

the global maximum for positive x occurs at x = 1/e for any n < 0; and the global minimum occurs at x = e^−1/n for any n > 0.

The infinite tetration

$x^{x^{x^{\cdot ^{\cdot ^{\cdot }}}}}$ or ${^{\infty }}x$

converges if and only if e^−e ≤ x ≤ e^1/e (or approximately between 0.0660 and 1.4447), due to a theorem of Leonhard Euler.

Number theory

The real number e is irrational. Euler proved this by showing that its simple continued fraction expansion is infinite. (See also Fourier's proof that e is irrational.)

Furthermore, by the Lindemann–Weierstrass theorem, e is transcendental, meaning that it is not a solution of any non-constant polynomial equation with rational coefficients. It was the first number to be proved transcendental without having been specifically constructed for this purpose (compare with Liouville number); the proof was given by Charles Hermite in 1873.

It is conjectured that e is normal, meaning that when e is expressed in any base the possible digits in that base are uniformly distributed (occur with equal probability in any sequence of given length).

Complex numbers

The exponential function e^x may be written as a Taylor series

$e^{x}=1+{x \over 1!}+{x^{2} \over 2!}+{x^{3} \over 3!}+\cdots =\sum _{n=0}^{\infty }{\frac {x^{n}}{n!}}$

Because this series is convergent for every complex value of x, it is commonly used to extend the definition of e^x to the complex numbers. This, with the Taylor series for sin and cos x, allows one to derive Euler's formula:

$e^{ix}=\cos x+i\sin x,$

which holds for every complex x. The special case with x = π is Euler's identity:

$e^{i\pi }+1=0,$

from which it follows that, in the principal branch of the logarithm,

$\ln(-1)=i\pi .$

Furthermore, using the laws for exponentiation,

$(\cos x+i\sin x)^{n}=\left(e^{ix}\right)^{n}=e^{inx}=\cos(nx)+i\sin(nx),$

which is de Moivre's formula.

The expression

$\cos x+i\sin x$

is sometimes referred to as cis(x).

The expressions of sin x and cos x in terms of the exponential function can be deduced:

$\sin x={\frac {e^{ix}-e^{-ix}}{2i}},\qquad \cos x={\frac {e^{ix}+e^{-ix}}{2}}.$

Differential equations

The family of functions

$y(x)=Ce^{x},$

where C is any real number, is the solution to the differential equation

$y'=y.$

Representations

Artikel utama: List of representations of e

The number e can be represented in a variety of ways: as an infinite series, an infinite product, a continued fraction, or a limit of a sequence. Two of these representations, often used in introductory calculus courses, are the limit

$e=\lim _{n\to \infty }\left(1+{\frac {1}{n}}\right)^{n},$

given above, and the series

$e=\sum _{n=0}^{\infty }{\frac {1}{n!}}$

obtained by evaluating at x = 1 the above power series representation of e^x.

Less common is the continued fraction

$e=[2;1,2,1,1,4,1,1,6,1,...,1,2n,1,...],$

which written out looks like

$e=2+{\cfrac {1}{1+{\cfrac {1}{2+{\cfrac {1}{1+{\cfrac {1}{1+{\cfrac {1}{4+{\cfrac {1}{1+{\cfrac {1}{1+\ddots }}}}}}}}}}}}}}.$

This continued fraction for e converges three times as quickly:

$e=1+{\cfrac {2}{1+{\cfrac {1}{6+{\cfrac {1}{10+{\cfrac {1}{14+{\cfrac {1}{18+{\cfrac {1}{22+{\cfrac {1}{26+\ddots }}}}}}}}}}}}}}.$

Many other series, sequence, continued fraction, and infinite product representations of e have been proved.

Stochastic representations

In addition to exact analytical expressions for representation of e, there are stochastic techniques for estimating e. One such approach begins with an infinite sequence of independent random variables X₁, X₂..., drawn from the uniform distribution on [0, 1]. Let V be the least number n such that the sum of the first n observations exceeds 1:

$V=\min \left\{n\mid X_{1}+X_{2}+\cdots +X_{n}>1\right\}.$

Then the expected value of V is e: E(V) = e.

Known digits

The number of known digits of e has increased substantially during the last decades. This is due both to the increased performance of computers and to algorithmic improvements.

Number of known decimal digits of e

Date	Decimal digits	Computation performed by
1690	1	Jacob Bernoulli
1714	13	Roger Cotes
1748	23	Leonhard Euler
1853	137	William Shanks
1871	205	William Shanks
1884	346	J. Marcus Boorman
1949	2,010	John von Neumann (on the ENIAC)
1961	100,265	Daniel Shanks and John Wrench
1978	116,000	Steve Wozniak on the Apple II

Since around 2010, the proliferation of modern high-speed desktop computers has made it feasible for most amateurs to compute trillions of digits of e within acceptable amounts of time. It currently has been calculated to 31,415,926,535,897 digits.

In computer culture

During the emergence of internet culture, individuals and organizations sometimes paid homage to the number e.

In an early example, the computer scientist Donald Knuth let the version numbers of his program Metafont approach e. The versions are 2, 2.7, 2.71, 2.718, and so forth.

In another instance, the IPO filing for Google in 2004, rather than a typical round-number amount of money, the company announced its intention to raise 2,718,281,828 USD, which is e billion dollars rounded to the nearest dollar.

Google was also responsible for a billboard that appeared in the heart of Silicon Valley, and later in Cambridge, Massachusetts; Seattle, Washington; and Austin, Texas. It read "{first 10-digit prime found in consecutive digits of e}.com". The first 10-digit prime in e is 7427466391, which starts at the 99th digit. Solving this problem and visiting the advertised (now defunct) website led to an even more difficult problem to solve, which consisted in finding the fifth term in the sequence 7182818284, 8182845904, 8747135266, 7427466391. It turned out that the sequence consisted of 10-digit numbers found in consecutive digits of e whose digits summed to 49. The fifth term in the sequence is 5966290435, which starts at the 127th digit. Solving this second problem finally led to a Google Labs webpage where the visitor was invited to submit a résumé.

Further reading

• Maor, Eli; e: The Story of a Number, ISBN 0-691-05854-7
• Commentary on Endnote 10 of the book Prime Obsession for another stochastic representation
• McCartin, Brian J. (2006). "e: The Master of All" (PDF). The Mathematical Intelligencer. 28 (2): 10–21. doi:10.1007/bf02987150. 

External links

• The number e to 1 million places and NASA.gov 2 and 5 million places
• e Approximations – Wolfram MathWorld
• Earliest Uses of Symbols for Constants Jan. 13, 2008
• "The story of e", by Robin Wilson at Gresham College, 28 February 2007 (available for audio and video download)
• e Search Engine 2 billion searchable digits of e, π and √2