Electrical engineering design with an evolutionary approach

ELECTRICAL ENGINEERING DESIGN WITH AN EVOLUTIONARY APPROACH Gregor Papa Computer Systems Department Jožef Stefan Institute, Ljubljana, Slovenia gregor.papa@ijs.si Barbara Koroušić Seljak Computer Systems Department Jožef Stefan Institute, Ljubljana, Slovenia barbara.korousic@ijs.si Jurij Šilc Computer Systems Department Jožef Stefan Institute, Ljubljana, Slovenia jurij.silc@ijs.si Abstract This paper presents two engineering design problems, both of which were solved by evolutionary algorithms. The evolutionary approach is used in universal electro-motor geometry optimization and integrated circuits area/time optimization. In the first case we improve the efficiency of a universal motor; where the goal is to find a new set of independent geometrical parameters for the rotor and the stator with the aim of reducing the motor’s power losses, which occur in the iron and the copper. In the second case we improve some parts of the high-level synthesis process of integrated circuits by considering the concurrency of operation scheduling and resource allocation constraints to ensure a globally optimal solution in a reasonable time. Keywords: Engineering design, Electro-motor, Integrated circuit, Evolutionary optimization 1. Introduction Evolutionary techniques are used in various search methods for a range of different optimization areas. Their undetermined approach gives them an advantage when it comes to multi-criteria problems and problems with more local 105 106 BIOINSPIRED OPTIMIZATION METHODS AND THEIR APPLICATIONS optima [8]. For this reason we adopted an artificial approach to the solving of our design problems using a genetic algorithm (GA) [2, 7]. The GA, as a frequent implementation of evolutionary techniques, is an optimization method based on the mechanism of evolution and natural genetics. This algorithm has already proved to be very efficient in a wide range of different optimization procedures where the exact equations are not available or some non-linearities are present [4]. In spite of its simplicity, the GA has proved to be an efficient method for solving various optimization and classification problems, in areas ranging from economics and game-theory to control-system design [3, 5, 9, 11, 12]. This paper presents two engineering design problems, both of which were solved with evolutionary algorithms. The evolutionary approach is used in universal electro-motor geometry optimization (UM design), and integrated circuits area/time optimization (IC design). 2. Problems in Engineering Design 2.1 Universal Motor Design Many common home appliances, such as vacuum cleaners and mixers, as well as power tools, such as drills and saws, are generally powered by a universal motor (UM) [16]. This type of motor has many advantages that make the UM such a popular choice for home appliances and power tools: a large output power in relation to its small size, high starting and running torque, variable speed that can be regulated in a simple way, and low manufacturing costs. Home appliances and power tools need as low an energy consumption, i.e., input power, as possible, while still satisfying the needs of the user by providing sufficient output power. The ratio of the output power to the input power defines the efficiency of the motor, which can be improved by reducing some of the main power losses in the motor, i.e., those that originate in the iron and the copper. This can be done by optimizing the geometry of both the rotor and the stator (see Fig. 1). Because of the high magnetic saturation of the iron in a UM the problem is a highly non-linear one. The rotor-and-stator unit of a UM is constructed by stacking the rotor/stator iron laminations. The shape and the profile of the rotor/stator lamination are described by several two-dimensional geometrical parameters. There are two types of parameter: the invariable and the variable. Invariable parameters are fixed; they cannot be altered, either for technical reasons or because of the physical constraints of the motor. Variable parameters are those that do not have predefined optimum values. Some of these variable parameters are mutually independent and without any constraints. In our case we optimize 12 mutually independent variable parameters. The efficiency of a UM is defined as the ratio of the output power P out to the input power Pinp , and it depends on various power losses, which include: Electrical Engineering Design with an Evolutionary Approach Figure 1. 107 Geometrical parameters of the stator and rotor of a UM. copper losses PCu , iron losses PF e , brush losses Pb , ventilation losses Pv , and friction losses Pf . When considering all the mentioned losses and the output power, the overall efficiency η of a UM can be defined as η= 2.2 Pout Pout = . Pinp Pout + PCu + PF e + Pb + Pv + Pf Design of Integrated Circuits High-level synthesis [6] is an automatic design process that transforms the initial behavioral description of the circuit (especially ASICs) into the final specification of the RTL. The process consists of the following: compilation, transformation, scheduling, allocation and binding. Of these, the operation scheduling and the resource allocation are the most important tasks of the highlevel synthesis because they are at the core of the design and crucially influence both the design and the final layout (see Fig. 2). Figure 2. Time/area optimized layout of an IC. 108 BIOINSPIRED OPTIMIZATION METHODS AND THEIR APPLICATIONS Due to the interdependence of these two tasks, the solution of one task depends on an estimation of the solution of the other task, which is not solved yet. The scheduling of the operation into different control steps therefore affects the allocation of operations to different units. The interaction of these two tasks presents formidable obstacles to the goal of optimization [1]. There are, however, some approaches to concurrent solving, but their solutions, to some extent, are less than optimal [10]. 3. The Genetic Algorithm in UM and IC Design When reducing the main power losses in a UM design by optimizing the geometry of the rotor/stator lamination we have to deal with a complex search space and its non-linear behavior. In IC design we apply the concurrency of interdependent tasks with their opponent constraints. Because traditional search-and-optimization methods have proved to be inefficient at finding the solution under such conditions, we decided to apply a GA. This heuristic method requires only a little information to provide a robust, yet flexible, search in a wide and complex search space. 3.1 UM Design Procedure Conventional motor design can be upgraded with a genetic algorithm. The advantages of this approach are that: there is no need for an experienced engineer to be present during the whole process, except at the beginning to decide on the initial design, and there is no need to know the mechanical and physical details of the problem. The problem can be solved without any knowledge of the problem, we only need some finite-element program to evaluate each solution. 3.1.1 Experimental Results. The proposed evolutionary design approach is evaluated by estimating the actual improvement in the efficiency of an initial UM that is designed using the conventional and evolutionary design approaches. We optimized the UM twice. The first one (Opt 1) was full optimization, where all parameters were optimized, while in the second case (Opt 2) we fixed the outer boundaries of the UM to get the design with the same amount of material and therefore the same initial material costs. We made prototypes of both the optimized and the costs-optimized motors and measured the real power losses and the efficiencies of the motors. These values are shown in Table 1. The results are only slightly different from those calculated with a finite-element program. The main reason for this difference can be explained by the non-exact calculation of the iron losses, due to a variation in the material’s properties. 109 Electrical Engineering Design with an Evolutionary Approach Table 1. UM evaluation results. Feature Analytical calculation Initial Opt 1 Opt 2 Prototype calculation Initial Opt 1 Opt 2 Pinp [W] Pout [W] ∆P = Pinp − Pout [W] Pout η= P [%] 1 044 731 313 70.0 1 050 730 320 69.5 inp ∆P improvement [W] η improvement [%] 3.2 970 731 239 75.8 982 731 251 74.8 74 5.8 62 4.8 990 730 260 73.7 1 000 730 270 73.0 60 4.2 50 3.5 IC Design Procedure The promising results of different evaluations [5, 11, 12] led us to the Evolutionary Concurrent Scheduling and Allocation (ECSA) design approach [10]. This approach considers scheduling and allocation constraints, allows a short design time and can find globally optimal solutions. The input description of the circuit is transformed into two basic (initial) schedules, obtained with the ASAP and ALAP algorithms. The functional units used in the first case are those that are the fastest for each operation, and in the second case are those that are the slowest for each operation. These two schedules present some kind of boundary solutions, since all the other solutions are executed in between the time limits defined by these two schedules. In other words, no other solution can be faster or slower, irrespective of the combinations of used units. Each solution has to be properly encoded, i.e., each operation’s start time and functional unit have to exist in the chromosome. The initial population is built upon the two initial solutions, which are multiplied to form the population with the so-called boundary solutions. The optimal solution has to be somewhere in-between the boundaries, therefore genetic operators (crossover, mutation, variation) transform those encoded solutions. With the transformations their start times and allocated functional units are changed. The appropriateness of the proposed approach is tested by a computer implementation of the ECSA algorithm, which is used with test-bench ICs. In addition to simple GA operators also the independent GA approach [10] was used. There is no need to preset some working parameters, e.g., the number of generations, the population size, and the probabilities of crossover, mutation and variation. These parameters are set automatically during the optimization phase, depending on the progress and the speed of the optimization. Setup. If the chromosome that represents a solution is large, then the population size also has to be large enough to ensure that many different 110 BIOINSPIRED OPTIMIZATION METHODS AND THEIR APPLICATIONS chromosomes will be involved in a search. The population size therefore depends on the size of the chromosome or the complexity of the problem. Crossover. Considering four candidates-two parents and their two offspringonly the first and the third, rated according to their fitness, pass to the next generation. This forces at least one of the offspring to be passed to the next generation in addition to the best candidate. Otherwise the offspring have only a small influence on new generations, since the crossing of two good parents probably produces offspring that are not so good. They might, however, be good after a few more transformations. Mutation. Chromosomes with low fitness are mostly exposed to mutation. Each position in the chromosome string is mutated if that position of the chromosome is of the same value in the majority of chromosomes in the population. This is the way to change the bad characteristics in "poorly fitted" chromosomes and to redirect the search to another direction. In the case of "well-fitted" chromosomes, values are mutated if they differ from the majority of values in other good chromosomes at the same position. This ensures faster convergence in the final stages of the optimization. Variation. The interchange of the values of two positions, as described for the basic operators, is performed if the frequency of the value in that position in the population of one position is high and the frequency of another bit is low. 3.2.1 Experimental Results. The ICs used for the evaluation are chosen on the basis of their appearance in the literature and similar studies. They differ in terms of size and the number of operation types. The ECSA algorithm is evaluated by a comparison with nearly optimal [15] force-directed scheduling (FDS) [14]. FDS tries to optimally schedule the DFG considering a uniform distribution the operations of the same type over the available control steps. 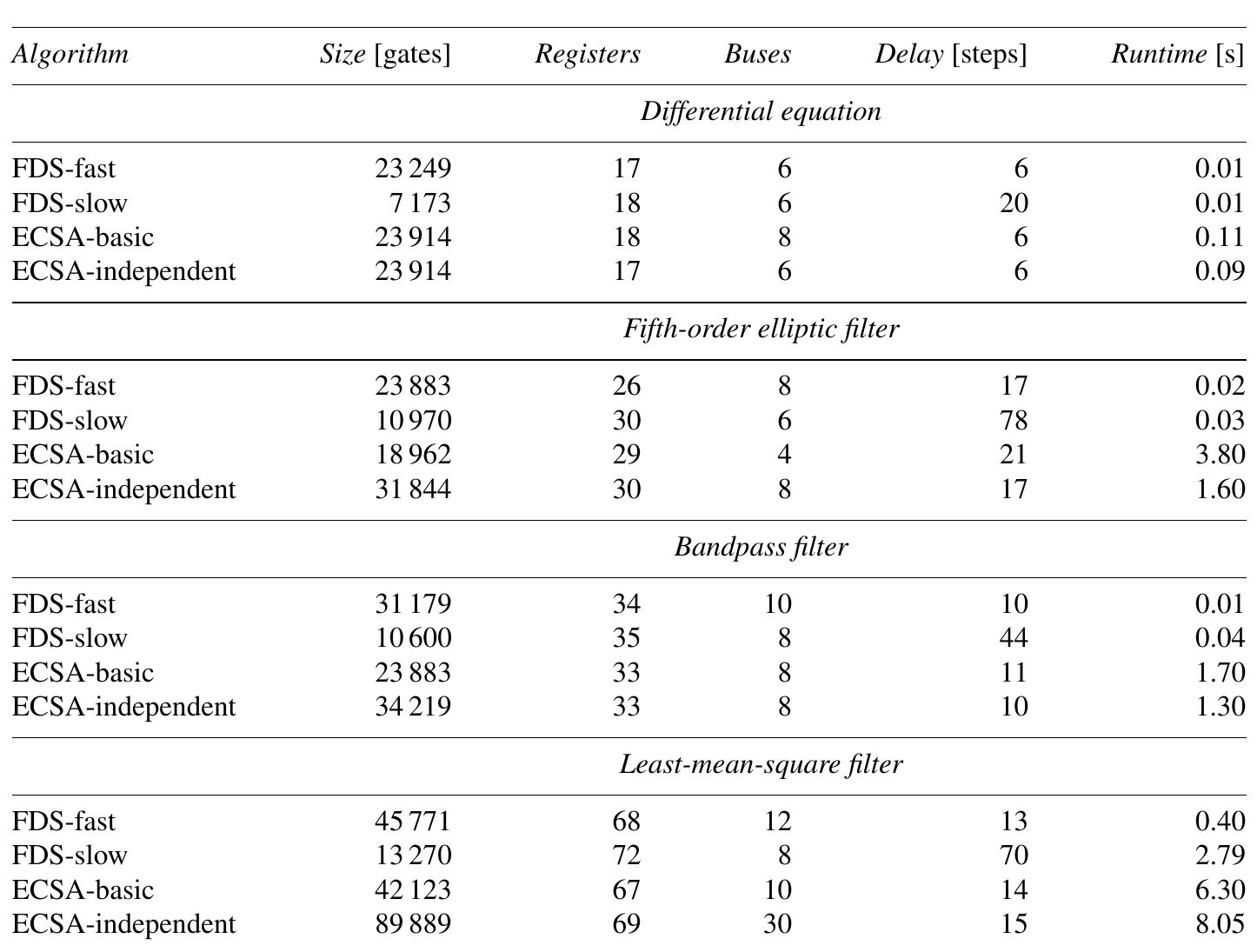Tables 2 and 3 show the results of the following evaluations: FDS with fast units, FDS with slow units, and ECSA with basic and independent genetic operators. There are two types of DFGs for each circuit. The first, or plain, is an ordinary data-flow graph with nodes that represent operations, as described in similar studies (Table 2); and the second, or improved [10], considers the input variables (start registers) via some additional nodes to ensure a more accurate estimation of the registers and the buses needed to implement the circuit (Table 3). Differential equation: Because of the small circuit size there is no improvement in the solutions obtained with the ECSA algorithm (either basic or independent) when considering an ordinary DFG-all the solutions are of a larger 111 Electrical Engineering Design with an Evolutionary Approach Table 2. The evaluation results of the ECSA algorithm with different test-bench ICs. Algorithm Size [gates] Registers Buses Delay [steps] Runtime [s] Differential equation FDS-fast FDS-slow ECSA-basic ECSA-independent 23 249 7 173 23 914 23 914 17 18 18 17 6 6 8 6 6 20 6 6 0.01 0.01 0.11 0.09 17 78 21 17 0.02 0.03 3.80 1.60 10 44 11 10 0.01 0.04 1.70 1.30 13 70 14 15 0.40 2.79 6.30 8.05 Fifth-order elliptic filter FDS-fast FDS-slow ECSA-basic ECSA-independent 23 883 10 970 18 962 31 844 26 30 29 30 8 6 4 8 Bandpass filter FDS-fast FDS-slow ECSA-basic ECSA-independent 31 179 10 600 23 883 34 219 34 35 33 33 10 8 8 8 Least-mean-square filter FDS-fast FDS-slow ECSA-basic ECSA-independent 45 771 13 270 42 123 89 889 68 72 67 69 12 8 10 30 size. But when we consider the start registers (input variables) there are some ECSA solutions with a slightly larger size and a smaller number of buses. Fifth-order elliptic filter: The evolutionary method with a basic approach finds a smaller circuit with a smaller number of buses and a slightly longer execution time for the ordinary DFG, whereas the independent approach could not find any improved solution. When dealing with the improved DFG, both approaches (basic and independent) find considerably smaller circuits with a slight increase in the execution time, while the independent approach also finds the solution with a substantial decrease in the required number of registers and buses. Bandpass filter: Both ECSA methods find, when dealing with the ordinary DFG, the solutions with a smaller number of registers and buses; the basic approach also finds the smaller circuit, but with a slightly longer execution time. When dealing with the improved DFG, both approaches find the solutions with the same circuit size and execution time as the comparable FDS solution, but the required number of registers and buses is considerably smaller for the ECSA solutions. 112 BIOINSPIRED OPTIMIZATION METHODS AND THEIR APPLICATIONS Table 3. The evaluation results of the ECSA algorithm with different test-bench ICs. Size [gates] Algorithm Registers Buses Delay [steps] Runtime [s] Differential equation with start registers FDS-fast FDS-slow ECSA-basic ECSA-independent 23 249 7 173 31 210 23 914 10 11 10 10 9 9 7 7 6 20 6 6 0.01 0.01 0.15 0.35 Fifth-order elliptic filter with start registers FDS-fast FDS-slow ECSA-basic ECSA-independent 23 883 10 970 18 962 15 922 21 25 24 18 16 16 16 9 17 78 19 21 0.02 0.04 4.80 3.40 10 44 10 10 0.02 0.04 2.40 2.90 Bandpass filter with start registers FDS-fast FDS-slow ECSA-basic ECSA-independent 31 179 10 600 31 179 31 179 25 26 23 23 23 23 19 19 Least-mean-square filter with start registers FDS-fast FDS-slow ECSA-basic ECSA-independent 45 771 13 270 45 220 63 517 33 37 32 33 29 27 25 25 13 70 13 13 0.48 3.52 9.20 12.30 Least-mean-square filter: At the expense of a small increase in the delay, the basic ECSA is able to decrease the size and lower the number of registers and buses of the ordinary DFG; but the independent ECSA is not able to improve any parameter. When dealing with the improved DFG, the basic ECSA is able to keep the initial delay, to decrease the circuit size and to lower the number of required registers and buses. The independent ECSA is only able to decrease the number of buses while increasing the circuit size. There are slightly longer runtimes when the ECSA algorithm is used. But considering the speed (a few seconds) and the evaluation presented in [13], where the runtimes for larger circuits increase enormously (exponentially) when the FDS algorithm is used, we can conclude that small and large circuits can be designed and optimized with the use of the proposed evolution-based algorithm, which exhibits a linear increase in the design time with an increase in circuit size. 4. Conclusions In the UM optimization we used an evolutionary approach to improve the efficiency of an electro-motor. The goal of our optimization was to find the new Electrical Engineering Design with an Evolutionary Approach 113 set of independent geometrical parameters of the rotor and the stator with the aim of reducing the motor’s power losses, which occur in the iron and the copper. The approach proves to be a simple and efficient search-and-optimization method for solving this day-to-day design problem in industry. It outperforms, by a significant improvement of the motor’s efficiency, a conventional design procedure that was used previously. By using the GA we are able to reduce the iron and the copper losses of an initial UM by at least 20%, and increasing the GA running time or setting its parameters more appropriately could improve on this result. In the IC area/time optimization we used an evolutionary approach to some parts of IC design. The work was focused on ASICs that need an even more sophisticated design due to their specific use. Optimally scheduled operations are not necessarily optimally allocated to functional units. To ensure optimum allocation we need to consider some allocation criteria while the scheduling is being done. The evolutionary approach considers scheduling and allocation constraints and ensures a globally optimal solution in a reasonable time. To evaluate our method we built an algorithm and implemented it with a computer. It is used with a group of test-bench ICs. These circuits are chosen because the same types were used in similar studies. The results of the evaluation of a computer-implemented algorithm show that the evolutionary methods are able to find a solution that is more appropriate in terms of all the considered and important objectives than is the case when working with classical deterministic methods. Acknowledgment The work presented in the paper was supported by the Slovenian Ministry of Education, Science and Sport (research programme P2-0098 Computer Structures and Systems), and partially by DOMEL, Electromotors and household devices, d. d., Železniki, Slovenia. References [1] J.R. Armstrong and F.G. Gray. VHDL Design: Representation and Synthesis. Prentice Hall PTR, 2000. [2] T. Bäck. Evolutionary Algorithms in Theory and Practice. Oxford University Press, New York, 1996. [3] D. Dasgupta and Z. Michalewicz. Evolutionary Algorithms in Engineering Applications. Springer-Verlag, 1997. [4] R. Drechsler. Evolutionary Algorithms for VLSI CAD. Kluwer Academic Publishers, 1998. [5] B. Filipič and J. Štrancar. Tuning EPR spectral parameters with a genetic algorithm. Applied Soft Computing, 1:83–90, 2001. [6] D.D. Gajski, N. Dutt, A. Wu, and S. Lin. High-Level Synthesis: Introduction to Chip and System Design. Kluwer Academic Publishers, 1992. 114 BIOINSPIRED OPTIMIZATION METHODS AND THEIR APPLICATIONS [7] D.E. Goldberg. Genetic Algorithms in Search, Optimization, and Machine Learning. Addison-Wesley, Reading, 1989. [8] C.L. Karr, I. Yakushin, and K. Nicolosi. Solving inverse initial-value, boundary-value problems via genetic algorithm. Engineering Applications of Artificial Intelligence, 13:625–633, 2000. [9] B. Koroušić-Seljak. Heuristic methods for a combinatorial optimization problem - realtime task scheduling problem. In Proceedings of the Artificial Networks in Engineering Conference (ANNIE’99), St. Louis, USA, 1999, pp. 1041–1046. [10] G. Papa. Concurrent operation scheduling and unit allocation with an evolutionary technique in the process of integrated-circuit design. Ph.D. thesis, Faculty of Electrical Engineering, University of Ljubljana, Slovenia, 2002. [11] G. Papa, B. Koroušić-Seljak, B. Benedičič, and T. Kmecl. Universal motor efficiency improvement using evolutionary optimization. IEEE Transactions on Industrial Electronics, 50:602–611, 2003. [12] G. Papa and J. Šilc. Automatic large-scale integrated circuit synthesis using allocationbased scheduling algorithm. Microprocessors and Microsystems, 26:139–147, 2002. [13] G. Papa, J. Šilc, and R. Wyrzykowski. Scheduling algorithms based on genetic approach. In Proceedings of the 4th Conference on Neural Networks and Their Application, Zakopane, Poland, 1999, pp. 469–474. [14] P.G. Paulin and J.P. Knight. Force-directed scheduling in automatic data path synthesis. In Proceedings of the 24th ACM/IEEE Design Automation Conference, Miami, USA, 1987, pp. 195–202. [15] P.G. Paulin and J.P. Knight. Scheduling and binding algorithms for high-level synthesis. In Proceedings of the 26th ACM/IEEE Design Automation Conference, Las Vegas, USA, 1989, pp. 1–6. [16] P.C. Sen. Principles of Electric Machines and Power Electronics. John Wiley & Sons, 1996.