Cyclotruncated simplectic honeycomb
In geometry, the cyclotruncated simplectic honeycomb (or cyclotruncated n-simplex honeycomb) is a dimensional infinite series of honeycombs, based on the symmetry of the 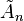 affine Coxeter group. It is given a Schläfli symbol t0,1{3[n+1]}, and is represented by a Coxeter-Dynkin diagram as a cyclic graph of n+1 nodes with two adjacent nodes ringed. It is composed of n-simplex facets, along with all truncated n-simplices.
affine Coxeter group. It is given a Schläfli symbol t0,1{3[n+1]}, and is represented by a Coxeter-Dynkin diagram as a cyclic graph of n+1 nodes with two adjacent nodes ringed. It is composed of n-simplex facets, along with all truncated n-simplices.
It is also called a Kagome lattice in two and three dimensions, although it is not a lattice.
In n-dimensions, each can be seen as a set of n+1 sets of parallel hyperplanes that divide space. Each hyperplane contains the same honeycomb of one dimension lower.
In 1-dimension, the honeycomb represents an apeirogon, with alternately colored line segments. In 2-dimensions, the honeycomb represents the trihexagonal tiling, with Coxeter graph ![]()
![]()
![]() . In 3-dimensions it represents the quarter cubic honeycomb, with Coxeter graph
. In 3-dimensions it represents the quarter cubic honeycomb, with Coxeter graph ![]()
![]()
![]() filling space with alternately tetrahedral and truncated tetrahedral cells. In 4-dimensions it is called a cyclotruncated 5-cell honeycomb, with Coxeter graph
filling space with alternately tetrahedral and truncated tetrahedral cells. In 4-dimensions it is called a cyclotruncated 5-cell honeycomb, with Coxeter graph ![]()
![]()
![]()
![]()
![]() , with 5-cell, truncated 5-cell, and bitruncated 5-cell facets. In 5-dimensions it is called an cyclotruncated 5-simplex honeycomb, with Coxeter graph
, with 5-cell, truncated 5-cell, and bitruncated 5-cell facets. In 5-dimensions it is called an cyclotruncated 5-simplex honeycomb, with Coxeter graph ![]()
![]()
![]()
![]()
![]() , filling space by 5-simplex, truncated 5-simplex, and bitruncated 5-simplex facets. In 6-dimensions it is called a cyclotruncated 6-simplex honeycomb, with Coxeter graph
, filling space by 5-simplex, truncated 5-simplex, and bitruncated 5-simplex facets. In 6-dimensions it is called a cyclotruncated 6-simplex honeycomb, with Coxeter graph ![]()
![]()
![]()
![]()
![]()
![]()
![]() , filling space by 6-simplex, truncated 6-simplex, bitruncated 6-simplex, and tritruncated 6-simplex facets.
, filling space by 6-simplex, truncated 6-simplex, bitruncated 6-simplex, and tritruncated 6-simplex facets.
| n | 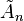 |
Name Coxeter diagram |
Vertex figure | Image and facets |
|---|---|---|---|---|
| 1 |  |
Apeirogon |
Yellow and cyan line segments |
|
| 2 |  |
Trihexagonal tiling |
 Rectangle |
 With yellow and blue equilateral triangles, and red hexagons |
| 3 |  |
quarter cubic honeycomb |
 Elongated triangular antiprism |
160px With yellow and blue tetrahedra, and red and purple truncated tetrahedra |
| 4 |  |
Cyclotruncated 5-cell honeycomb |
120px Elongated tetrahedral antiprism |
5-cell, truncated 5-cell, bitruncated 5-cell |
| 5 | 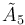 |
Cyclotruncated 5-simplex honeycomb |
120px | 5-simplex, truncated 5-simplex, bitruncated 5-simplex |
| 6 | 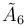 |
Cyclotruncated 6-simplex honeycomb |
6-simplex, truncated 6-simplex, bitruncated 6-simplex, tritruncated 6-simplex |
|
| 7 | 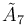 |
Cyclotruncated 7-simplex honeycomb |
7-simplex, truncated 7-simplex, bitruncated 7-simplex |
|
| 8 |  |
Cyclotruncated 8-simplex honeycomb |
8-simplex, truncated 8-simplex, bitruncated 8-simplex, tritruncated 8-simplex, quadritruncated 8-simplex |
Projection by folding
The cyclotruncated (2n+1)- and 2n-simplex honeycombs and (2n-1)-simplex honeycombs can be projected into the n-dimensional hypercubic honeycomb by a geometric folding operation that maps two pairs of mirrors into each other, sharing the same vertex arrangement:
 |
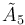 |
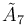 |
 |
 |
... | |||||
|---|---|---|---|---|---|---|---|---|---|---|
 |
 |
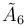 |
 |
 |
... | |||||
 |
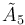 |
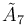 |
 |
... | ||||||
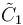 |
 |
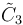 |
 |
 |
... |
See also
- Hypercubic honeycomb
- Alternated hypercubic honeycomb
- Quarter hypercubic honeycomb
- Simplectic honeycomb
- Omnitruncated simplectic honeycomb
References
- George Olshevsky, Uniform Panoploid Tetracombs, Manuscript (2006) (Complete list of 11 convex uniform tilings, 28 convex uniform honeycombs, and 143 convex uniform tetracombs)
- Branko Grünbaum, Uniform tilings of 3-space. Geombinatorics 4(1994), 49 - 56.
- Norman Johnson Uniform Polytopes, Manuscript (1991)
- Coxeter, H.S.M. Regular Polytopes, (3rd edition, 1973), Dover edition, ISBN 0-486-61480-8
- Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1]
- (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380-407, MR 2,10] (1.9 Uniform space-fillings)
- (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
| Fundamental convex regular and uniform honeycombs in dimensions 2–10 | |||||
|---|---|---|---|---|---|
| Family | 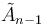 |
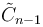 |
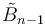 |
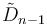 |
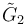 / / 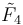 / / 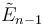 |
| Uniform tiling | {3[3]} | δ3 | hδ3 | qδ3 | Hexagonal |
| Uniform convex honeycomb | {3[4]} | δ4 | hδ4 | qδ4 | |
| Uniform 5-honeycomb | {3[5]} | δ5 | hδ5 | qδ5 | 24-cell honeycomb |
| Uniform 6-honeycomb | {3[6]} | δ6 | hδ6 | qδ6 | |
| Uniform 7-honeycomb | {3[7]} | δ7 | hδ7 | qδ7 | 222 |
| Uniform 8-honeycomb | {3[8]} | δ8 | hδ8 | qδ8 | 133 • 331 |
| Uniform 9-honeycomb | {3[9]} | δ9 | hδ9 | qδ9 | 152 • 251 • 521 |
| Uniform n-honeycomb | {3[n]} | δn | hδn | qδn | 1k2 • 2k1 • k21 |