点連結度
点連結度
出典: フリー百科事典『ウィキペディア(Wikipedia)』 (2021/01/24 09:47 UTC 版)
グラフ G から取り除くと非連結になるような k 個の頂点集合をk-点切断とよぶ。G においてk-点切断の最小サイズを点連結度または連結度とよび、 κ ( G ) , χ ( G ) {\displaystyle \kappa (G),\chi (G)} で表す。特に、1-点切断を切断点 (cut vertex) または関節点 (articulation point) とよぶ。k-連結グラフ (k-connected graph) は点連結度が k 以上のグラフである。 G から S を取り除いたグラフにおいて x と y の間に道が存在しないことを頂点の集合 S が x, y を分離するという。グラフ G から(もし存在すれば)辺 xy を除いたグラフにおいて、二つの頂点 x, y を分離するために必要な頂点の個数を s とするこのとき、x, yが隣接していないなら s を、x, y が隣接しているなら s + 1 を x, y の局所連結度といい、κ(x, y) 等で表すことが多い。点連結度は局所連結度の最小値と一致する。 グラフ G のある因子が k連結なら、G 自身も k 連結となる。G が k 連結で、G の自分自身を除いた因子が k 連結でないとき(つまり、G から一つでも辺を取り除くと k 連結でないとき)、G を 極小 k 連結 (minimally k-connected) という。
※この「点連結度」の解説は、「連結グラフ」の解説の一部です。
「点連結度」を含む「連結グラフ」の記事については、「連結グラフ」の概要を参照ください。
点連結度と同じ種類の言葉
- 点連結度のページへのリンク
 の点の
の点の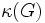 は点
は点