部分集合とは？ わかりやすく解説

読み方：ぶぶんしゅうごう

「部分集合」とは、1つの集合が他の1つの集合と重なる部分を持つことを意味する表現である。

「部分集合」の基本的な意味

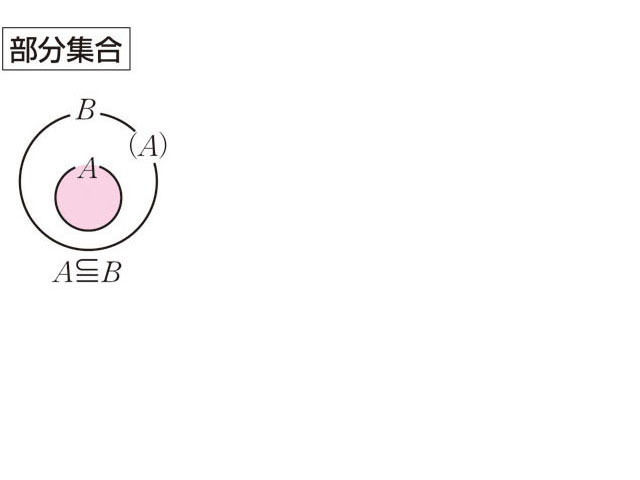
「部分集合」とは、数学で用いられる概念の1つで集合論で使用されることが多い言葉だ。集合論で用いられている記号は、同じ使用法で論理学でも用いられている。「部分集合」は以下の例文のように表現することが可能だ。A⊆B（AはBに含まれる）。この場合Aの方が集合を構成する要素に当たる。集合を構成する要素のことは、元（げん）と呼ぶこともできる。部分集合ではAとBとが完全に一致してもよい。もし不完全に一致している場合には、「部分集合」ではなく真部分集合と呼ばれる。「部分集合」の個数を求めたいときには、重複順列を使用すると簡単に導き出せる。

「部分集合」の発音・読み方

「部分集合」の読み方は、ぶぶんしゅうごうである。「部分集合」を表現するときには、A⊆Bのようにかけばよい。A⊆Bは「AはBに含まれる」と同義である。

「部分集合」の語源・由来

「部分集合」は集合論の中で用いられ始めた用語である。つまり「部分集合」を一般に普及させたのは、集合論を生み出した人間だと考えることができる。集合論はロシアの数学者、ゲオルク・カントールが作り出したとされている。ただ表記は現在の形ではなかったと違ったようだ。最初に現在の形で著作にまとめたのはドイツの数学者リヒャルト・デデキントである。デデキントは1872年の著作『数について』で、部分集合を表すのに⊂という記号を用いた。それ以前には「＞＜」のような不等号が「部分集合」を表す時に使用されていた。

「部分集合」に関連する用語の解説

ここでは「部分集合」に関連する用語のいくつかを、解説していく。

空集合とは

空集合は、要素を1つも含まない集合のことを指す言葉だ。何も含むことのない集合と言いかえることもできる。集合と呼ばれるものはすべて、空集合を部分集合として持っている。数学の場で用いるときは専用の記号を用いるが、「｛｝」のような中括弧で代用可能だ。コンピューターなどで文字の使用が限定されているときには、「ファイ」が用いられることもある。

真部分集合とは

真部分集合とは、1つの集合の要素がすべてもう1つの集合の中に入っており、その上で1つの集合に別の要素が含まれていることを指す。1つの集合に全く他の要素が含まれていない場合には、真部分集合ではなく「部分集合」と言う。

共通部分とは

共通部分を英語で表す時には、intersectionとするといい。その意味するところは、与えられた集合の中で全てに共通する要素を含みながらそれ以外の要素をもたない集合のこととなる。共通部分は、共通集合・交差・交わり・積集合・積と表現することもできる。ただ積集合と表記する場合は直積集合の意味で用いられていることが多いので、注意が必要だ。

和集合とは

和集合とは、集合の集まりに対してそれらの集合の中の少なくとも一部が含まれている集合を合わせたもののことである。別の言い方としては、合併集合・合併・結びなどを挙げることができる。和集合を表す記号は「∪」で、A∪Bと表す。日本語にするときには、AまたはBという言葉を当てるとよい。

「部分集合」の使い方・例文

「部分集合」は数学や論理学で主に用いられる言葉である。専門的な用語ではあるが、汎用性もあるので日常会話で用いられることも多い。実際に文章内で使用されるときには、「部分集合は集合論の部門の1つだ」・「私の全ては音楽でできている、したがって私は音楽の部分集合なのだ」のように用いるといい。

「部分集合」の英訳

「部分集合」は数学の用語である。数学は国際的な学問であるから、英語に翻訳することが比較的簡単だ。この言葉を英訳する場合には、a subsetを用いるとよい。実際に文章の中で用いるときには、「A is a subset of B（AはBの部分集合である）」のように用いることができる。